
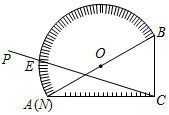
 如圖,量角器的直徑與直角三角板ABC的斜邊AB重合,其中量角器0刻度線的端點N與點A重合,射線CP從CA處出發(fā)沿順時針方向以每秒2度的速度旋轉,CP與量角器的半圓弧交于點E,第23秒時,點E在量角器上對應的度數(shù)是92度.
如圖,量角器的直徑與直角三角板ABC的斜邊AB重合,其中量角器0刻度線的端點N與點A重合,射線CP從CA處出發(fā)沿順時針方向以每秒2度的速度旋轉,CP與量角器的半圓弧交于點E,第23秒時,點E在量角器上對應的度數(shù)是92度. 分析 先連接OE,由∠ACB=90°,根據(jù)圓周角定理,可得點C在⊙O上,即可得∠EOA=2∠ECA,又由∠ECA的度數(shù),繼而求得答案.
解答 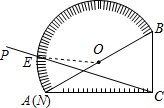 解:連接OE,
解:連接OE,
∵射線CP從CA處出發(fā)沿順時針方向以每秒2度的速度旋轉,
∴第23秒時,∠ACE=2°×23=46°,
∵∠ACB=90°,
∴點C在以AB為直徑的圓上,
即點C在⊙O上,
∴∠EOA=2∠ECA=2×46°=92°.
故答案為:92.
點評 此題考查了圓周角定理,在同圓或等圓中,同弧或等弧所對的圓周角相等,都等于這條弧所對的圓心角的一半.解題的關鍵是證得點C在⊙O上,注意輔助線的作法以及數(shù)形結合思想的運用.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:解答題
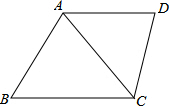 如圖,梯形ABCD中,AD∥BC,AC為對角線,且∠DCA=∠B,線段AD、BC的長是方程x(x-4)+2(4-x)=0的兩根,且AD<BC,CD=3,求AB與AC的長.
如圖,梯形ABCD中,AD∥BC,AC為對角線,且∠DCA=∠B,線段AD、BC的長是方程x(x-4)+2(4-x)=0的兩根,且AD<BC,CD=3,求AB與AC的長.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,在△ABC中,AC=8,D、E分別為AB、AC的中點,F(xiàn)為線段DE上一點,連接AF、CF使AF⊥CF,且DF=1.若△ADF面積為2,則△ABC的面積為( )
如圖,在△ABC中,AC=8,D、E分別為AB、AC的中點,F(xiàn)為線段DE上一點,連接AF、CF使AF⊥CF,且DF=1.若△ADF面積為2,則△ABC的面積為( )| A. | 25 | B. | 30 | C. | 35 | D. | 40 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
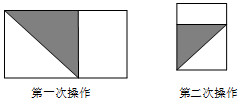 將長為1,寬為a的長方形紙片$({\frac{1}{2}<a<1})$如圖那樣折一下,剪下一個邊長等于長方形的寬度的正方形(稱為第一次操作);再把剩下的長方形如圖那樣折一下,剪下一個邊長等于此時長方形寬度的正方形(稱為第二次操作);如些反復操作下去,若在第n次操作后剩下的長方形為正方形,則操作終止.
將長為1,寬為a的長方形紙片$({\frac{1}{2}<a<1})$如圖那樣折一下,剪下一個邊長等于長方形的寬度的正方形(稱為第一次操作);再把剩下的長方形如圖那樣折一下,剪下一個邊長等于此時長方形寬度的正方形(稱為第二次操作);如些反復操作下去,若在第n次操作后剩下的長方形為正方形,則操作終止.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 節(jié)約能源,保護生態(tài),迎接低碳時代的到來,某紙品加工廠利用邊角線裁出正方形和長方形兩種硬紙片,制作甲、乙兩種無蓋的長方體紙盒出售給禮品店.
節(jié)約能源,保護生態(tài),迎接低碳時代的到來,某紙品加工廠利用邊角線裁出正方形和長方形兩種硬紙片,制作甲、乙兩種無蓋的長方體紙盒出售給禮品店.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,點E在?ABCD的邊AD上,沿BE折疊,點A落在邊CD上的點F處,若△FDE的周長為8,△FCB的周長為22.求FC的長.
如圖,點E在?ABCD的邊AD上,沿BE折疊,點A落在邊CD上的點F處,若△FDE的周長為8,△FCB的周長為22.求FC的長.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com