
分析 (1)設降價x元,根據“利潤率不低于10%”列出不等式求解即可;
(2)設m%=a,根據“A商品在3月15日那一天賣出的數量就比原來一周賣出的數量增加了$\frac{12}{5}$m%,這樣一天的利潤達到了20000元”列出方程求得a后即可求得m的值.
解答 解:(1)設降價x元,列不等式為(800×0.9-x)≥500(1+10%),
解得:x≤170,
答:問最多降價170元,才能使利潤率不低于10%;
(2)設m%=a,根據題意得:[800(1+3a)-2600a-500]•50(1+$\frac{12}{5}$a)=20000,
整理得:24a2-26a+5=0,
解得:a1=$\frac{5}{6}$,a2=$\frac{1}{4}$(舍去),
∴m%=$\frac{5}{6}$,
∴m=$\frac{250}{3}$.
點評 本題考查了一元二次方程的應用及一元一次不等式的應用,解題的關鍵是從題目中整理出等量關系和不等關系,難度不大.


科目:初中數學 來源: 題型:解答題
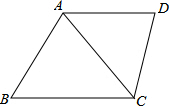 如圖,梯形ABCD中,AD∥BC,AC為對角線,且∠DCA=∠B,線段AD、BC的長是方程x(x-4)+2(4-x)=0的兩根,且AD<BC,CD=3,求AB與AC的長.
如圖,梯形ABCD中,AD∥BC,AC為對角線,且∠DCA=∠B,線段AD、BC的長是方程x(x-4)+2(4-x)=0的兩根,且AD<BC,CD=3,求AB與AC的長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
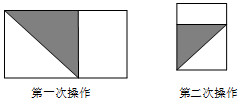 將長為1,寬為a的長方形紙片$({\frac{1}{2}<a<1})$如圖那樣折一下,剪下一個邊長等于長方形的寬度的正方形(稱為第一次操作);再把剩下的長方形如圖那樣折一下,剪下一個邊長等于此時長方形寬度的正方形(稱為第二次操作);如些反復操作下去,若在第n次操作后剩下的長方形為正方形,則操作終止.
將長為1,寬為a的長方形紙片$({\frac{1}{2}<a<1})$如圖那樣折一下,剪下一個邊長等于長方形的寬度的正方形(稱為第一次操作);再把剩下的長方形如圖那樣折一下,剪下一個邊長等于此時長方形寬度的正方形(稱為第二次操作);如些反復操作下去,若在第n次操作后剩下的長方形為正方形,則操作終止.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 節約能源,保護生態,迎接低碳時代的到來,某紙品加工廠利用邊角線裁出正方形和長方形兩種硬紙片,制作甲、乙兩種無蓋的長方體紙盒出售給禮品店.
節約能源,保護生態,迎接低碳時代的到來,某紙品加工廠利用邊角線裁出正方形和長方形兩種硬紙片,制作甲、乙兩種無蓋的長方體紙盒出售給禮品店.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com