
分析 (1)將點N(0,-3)代入y=-ax2+bx+3a求得a的值,然后再將點M的坐標代入可求得b的值與可得到二次函數C1的解析式,然后通過配方可得到C1的頂點坐標,然后由C1與C2關于原點對稱可得到二次函數C2的解析式;
(2)先根據題意畫出圖形,然后再求得點B、C、D的坐標,接下來,依據兩點間的距離公式求得CD2、BC2、DB2的值,最后依據勾股定理的逆定理進行證明即可;
(3)當CD=DP時,依據二次函數和等腰三角形的對稱性可求得點P的坐標,當點P在CD的垂直平分線上時,可先求得CD的解析式,然后再求得CD的垂直平分線EP的解析式,然后求得PE與拋物線的交點坐標即可;根據圖形可知CP>CD,故此不存在CD=PC的情況.
解答 解:(1)將點N(0,-3)代入y=-ax2+bx+3a得:3a=-3,解得a=-1,
∴二次函數C1:y=x2+bx-3.
將M(1,0)代入拋物線的解析式得:1+b-3=0,解得b=2.
∴二次函數C1:y=x2+2x-3=(x+1)2-4.
∵二次函數C1與二次函數C2關于原點對稱,
∴二次函數C2:y=-(x-1)2+4.
(2)如圖1所示: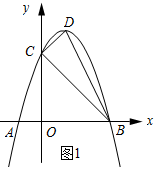
∵二次函數C2:y=-(x-1)2+4.
∴D(1,4).
∵當x=0時,y=3,
∴C(0,3).
∵令y=0得-(x-1)2+4=0,解得x=3或x=-1,
∴B(3,0),A(-1,0).
∵依據兩點間的距離公式可知CD2=(1-0)2+(4-3)2=2,BC2=(3-0)2+(3-0)2=18;BD2=(3-1)2+(4-0)2=20,
∴CD2+BC2=BD2.
∴△BCD是直角三角形.
(3)存在.
理由:①如圖2所示: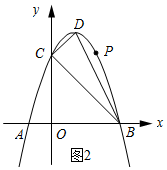
由拋物線的對稱性質可知:當點P與點C關于x=1對稱時,△CDP為等腰三角形,
∴P(2,3).
②如圖3所示:當點P在CD的垂直平分線上時,△CDP為等腰三角形.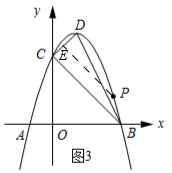
設CD的解析式為y=kx+3,將點D的坐標代入得:k+3=4,解得:k=1.
由中點坐標公式可知E(0.5,3.5)
∴直線PE的解析式y=-x+b,將E(0.5,3.5)代入得:-0.5+b=3.5,解得:b=4,
∴直線PE的解析式為y=-x+4.
將y=-x+4與y=-(x-1)2+4聯立,解得:x=$\frac{3+\sqrt{5}}{2}$或x=$\frac{3-\sqrt{5}}{2}$(舍去)
∴y=-x+4=$\frac{5-\sqrt{5}}{2}$.
∴點P的坐標為($\frac{3+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$).
③∵當點P作點D右側的拋物線上運動時,PC>PD,
∴不存在PC=PD的情況.
綜上所述,點P的坐標為P(2,3)或($\frac{3+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$)時,△PCD為等腰三角形.
點評 本題主要考查的是二次函數的綜合應用,解答本題主要應用了待定系數法求二次函數的解析式,兩點間的距離公式,勾股定理的逆定理,分類討論是解答本題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
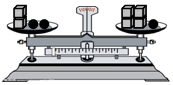 如圖,一個平衡的天平盤中,左盤有2個小正方體和2個小球,右盤有4個小正方體和1個小球.每個小球的重量用x克表示,小正方體每個5克,那么可列方程得2×5+2x=4×5+x.
如圖,一個平衡的天平盤中,左盤有2個小正方體和2個小球,右盤有4個小正方體和1個小球.每個小球的重量用x克表示,小正方體每個5克,那么可列方程得2×5+2x=4×5+x.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com