

分析 (1)連接PC,根據三角形的一個外角等于與它不相鄰的兩個內角的和可得∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,再表示出∠1+∠2即可;
(2)連接PC,方法與(1)相同;
(3)利用三角形的一個外角等于與它不相鄰的兩個內角的和討論求解即可.
解答 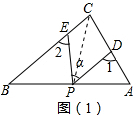 解:(1)如圖(1),連接PC,
解:(1)如圖(1),連接PC,
由三角形的外角性質,∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,
∵∠DPE=∠α=50°,∠C=90°,
∴∠1+∠2=50°+90°=140°,
故答案為:140°;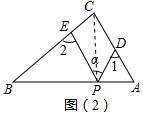
(2)∠1+∠2=90°+∠α;理由如下:
連接PC,如圖(2),
由三角形的外角性質,∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,
∵∠C=90°,∠DPE=∠α,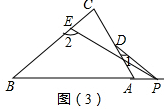
∴∠1+∠2=90°+∠α;
(3)∠2-∠1=90°+∠α或∠2-∠1=90°-α.理由如下:
分情況討論:
①如圖(3),由三角形的外角性質得:∠2=∠C+∠1+∠α,
∴∠2-∠1=90°+∠α;
②當P點運動至ED的延長線時,E,D,P三點共線,
此時∠DPE=0°,
∴∠2-∠1=90°+∠α;
③當P點繼續向右運動,此時EP在DP上方,
則∠2-90°=∠1-α,
∴∠2-∠1=90°-α;
綜上所述:∠α、∠1、∠2之間的關系為∠2-∠1=90°+∠α或∠2-∠1=90°-α.
點評 此題是三角形綜合題,主要考查了四邊形的內角和,三角形的內角和,三角形的外角的性質,平角的定義,解本題的關鍵是將∠1,∠2,α轉化到一個三角形或四邊形中,是一道比較簡單的中考常考題.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
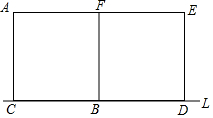 如圖,已知邊長等于8個單位長度的兩個完全相同的正方形ACBF、BDEF有公共邊BF,且CB與BD均在直線L上,將正方形ACBF沿直線L以1單位/秒向右平移,設移動時間為t秒,正方形ACBF在移動過程中與正方形BDEF重疊的面積為S,試求:
如圖,已知邊長等于8個單位長度的兩個完全相同的正方形ACBF、BDEF有公共邊BF,且CB與BD均在直線L上,將正方形ACBF沿直線L以1單位/秒向右平移,設移動時間為t秒,正方形ACBF在移動過程中與正方形BDEF重疊的面積為S,試求:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
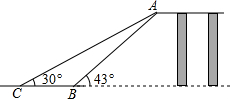 如圖是某工廠貨物傳送帶的平面示意圖,為提高傳送過程的安全性,工廠計劃改造傳動帶與地面的夾角,使其AB的坡角由原來的43°改為30°.已知原傳送帶AB長為5米.求新舊貨物傳送帶著地點B、C之間相距多遠?(結果保留整數,參考數據:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如圖是某工廠貨物傳送帶的平面示意圖,為提高傳送過程的安全性,工廠計劃改造傳動帶與地面的夾角,使其AB的坡角由原來的43°改為30°.已知原傳送帶AB長為5米.求新舊貨物傳送帶著地點B、C之間相距多遠?(結果保留整數,參考數據:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com