Question

3．操作實驗：如圖，把等腰三角形沿頂角平分線對折折疊后，發現被折疊分成的兩個三角形成軸對稱，所以△ABO≌△ACD，所以∠B=∠C．

歸納結論：如果一個三角形的兩條邊相等，那么這兩條邊所對的角也相等，
根據上述內容：如圖（4），在△ABC中，AB=AC，試說明∠B=∠C的理由
探究應用：如圖（5），CB⊥AB，垂足為B，DA⊥AE垂足為A，E為AB的中點，AB=BC，CE⊥BD．
（1）BE與AD是否相等？為什么？
（2）小明認為AC是線段DE的垂直平分線，你認為對嗎？說說你的理由？
（3）∠DBC與∠DCB相等嗎？試說明理由．
（4）某超市舉行有獎促銷活動；凡一次性購物滿300元者，即可獲得一次搖獎機會，搖獎機是一個圓形轉盤（如圖6所示），被分成16等分，搖中紅、黃、藍色區域，分獲一、二、三等獎，獎金一次為60、50、40元，一次性購物滿300元者，如果不搖獎可返還現金15元．
①搖獎一次，獲一等獎的概率是多少
②若李一次性購物滿了300元，他是參與搖獎劃算還是領15元現金劃算，請你幫他算算．

Answer 1

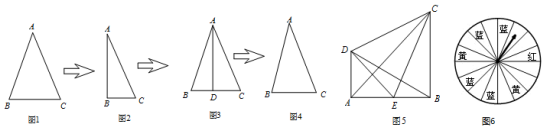
分析 歸納結論：作等腰三角形底邊上的高，構造全等三角形．
探究應用：（1）BE與AD在兩個直角三角形中，證這兩個直角三角形全等即可；
（2）可證點A，C在線段DE的垂直平分線上．注意結合（1）的結論，利用全等證明即可；
（3）由第二問的垂直平分線的性質，得到CD=CE，由第一問的全等得到DB=CE，那么CD=BD，所以∠DBC=∠DCB；
（4）①找到紅色區域的份數占總份數的多少即為獲得一等獎的概率，
②游戲是否合算，關鍵要看游戲雙方獲勝的機會是否相等，即判斷雙方取勝的概率是否相等，或轉化為在總情況明確的情況下，判斷雙方取勝所包含的情況數目是否相等．

解答 解：思考驗證：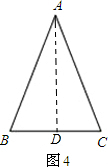

過A點作AD⊥BC于D，
∴∠ADB=∠ADC=90°，
在Rt△ABD和Rt△ACD中，$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\end{array}\right.$，
∴△ABD≌△ACD（HL），
∴∠B=∠C；

探究應用：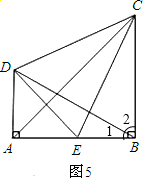

（1）說明：因為BD⊥EC，
∴∠CEB+∠1=90°，
∠1+∠ADB=90°，
∴∠ADB=∠BEC，
在△ADB和△BEC中$\left\{\begin{array}{l}{∠ADB=∠BEC}\\{AB=BC}\\{∠DAB=∠EBC=90°}\end{array}\right.$，
∴△DAB≌△EBC（ASA）．
∴DA=BE．

（2）∵E是AB中點，
∴AE=BE．
∵AD=BE，
∴AE=AD．
在△ABC中，因為AB=BC，
∴∠BAC=∠BCA．
∵AD∥BC，
∴∠DAC=∠BCA．
∴∠BAC=∠DAC．
在△ADC和△AEC中，$\left\{\begin{array}{l}{AD=AE}\\{∠DAC=∠EAC}\\{AC=AC}\end{array}\right.$，
∴△ADC≌△AEC（SAS）．
∴DC=CE．
∴C在線段DE的垂直平分線上．
∵AD=AE，
∴A在線段DE的垂直平分線上．
∴AC垂直平分DE．

（3）∵AC是線段DE的垂直平分線，
∴CD=CE．
∵△ADB≌△BEC，
∴DB=CE．
∴CD=BD．
∴∠DBC=∠DCB；

（4）①整個圓周被分成了16份，紅色為1份，
∴獲得一等獎的概率為：$\frac{1}{16}$，

②轉轉盤：60×$\frac{1}{16}$+50×$\frac{2}{16}$+40×$\frac{4}{16}$=20元，
∵20元＞15元，
∴轉轉盤劃算．

點評 此題是三角形綜合題，主要考查了全等三角形的判定和性質，等腰直角三角形的判定和性質，解本題的關鍵是作出作∠BAC的角平分線AD判斷∠B=∠C．