
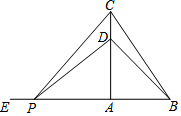
 如圖,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,點D在線段AC上,且CD=1 cm,動點P從BA的延長線上距A點5 cm的E點出發,以每秒2 cm的速度沿射線EA的方向運動了t秒.
如圖,在△ABC中,∠BAC=90°,AB=3 cm,BC=5 cm,點D在線段AC上,且CD=1 cm,動點P從BA的延長線上距A點5 cm的E點出發,以每秒2 cm的速度沿射線EA的方向運動了t秒.分析 (1)根據題意可得PE=2t.
(2)當PA=AC=4時,△ABC≌△ADP,可得方程5-2t=4或2t-5=4,解方程即可.
(3)分兩種情形討論即可①當0<t≤4時.②當t>4時,分別求解即可.
解答 解:(1)由題意PE=2t.
故答案為2t.
(2)存在.
理由:在Rt△ABC中,∵AB=3,BC=5,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵CD=1,
∴AD=AB=3,
在△ABC和△PAD中,
∵∠BAC=∠DAP=90°,AD=BC,
∴當PA=AC=4時,△ABC≌△ADP,
∴5-2t=4或2t-5=4,
∴t=$\frac{1}{2}$s或$\frac{9}{2}$s.
∴∴t=$\frac{1}{2}$s或$\frac{9}{2}$s時,使△ABC與以A、D、P為頂點的三角形全等.
(3)①當0<t≤4時,S=$\frac{1}{2}$PB•AC=$\frac{1}{2}$•(8-2t)•4=16-4t.
②當t>4時,S=S=$\frac{1}{2}$PB•AC=$\frac{1}{2}$•(2t-8)•4=4t-16.
綜上所述,S=$\left\{\begin{array}{l}{16-4t}&{(0<t≤4)}\\{4t-16}&{(t>4)}\end{array}\right.$.
點評 本題考查三角形綜合題、全等三角形的判定和性質、三角形的面積等知識,解題的關鍵是學會用分類討論的思想思考問題,注意一題多解,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
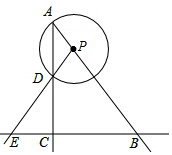 Rt△ABC,∠ACB=90°,AC=4,BC=3,P是射線AB上的一個動點,以P為圓心,PA為半徑的圓P與射線AC的另一個交點為D,直線PD交BC于點E.
Rt△ABC,∠ACB=90°,AC=4,BC=3,P是射線AB上的一個動點,以P為圓心,PA為半徑的圓P與射線AC的另一個交點為D,直線PD交BC于點E.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x≤3 | B. | x≠4 | C. | x≥3或x≠4 | D. | x≤3或x≠4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 方式一 | 方式二 | |
| 月租費 | 30元/月 | 0 |
| 本地通話費 | 0.20元/分鐘 | 0.40元/分鐘 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 甲種客車 | 乙種客車 | |
| 載客量(人/輛) | 45 | 30 |
| 租金(元/輛) | 500 | 320 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,己知AB是半徑為2的圓O直徑,C是圓上一點,D是BC延長線上一點,過點D的直線交AC于E點,且△AEF為等邊三角形.
如圖,己知AB是半徑為2的圓O直徑,C是圓上一點,D是BC延長線上一點,過點D的直線交AC于E點,且△AEF為等邊三角形.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
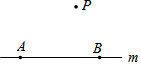 如圖,點A,B在直線m上,點P在直線m外,點Q是直線m上異于點A,B的任意一點,則下列說法或結論正確的是( )
如圖,點A,B在直線m上,點P在直線m外,點Q是直線m上異于點A,B的任意一點,則下列說法或結論正確的是( )| A. | 射線AB和射線BA表示同一條射線 | |
| B. | 線段PQ的長度就是點P到直線m的距離 | |
| C. | 連接AP,BP,則AP+BP>AB | |
| D. | 不論點Q在何處,AQ=AB-BQ或AQ=AB+BQ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y2<y3<y1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com