
分析 設AB、BC、AC與⊙O的切點分別為D、F、E;易證得四邊形OECF是正方形;那么根據切線長定理可得:CE=CF=$\frac{1}{2}$(AC+BC-AB),由此可求出r的長.
解答 解:如圖: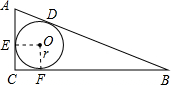
在Rt△ABC,∠C=90°,AC=5,BC=12,
根據勾股定理AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
四邊形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°,
∴四邊形OECF是正方形,
由切線長定理,得:AD=AE,BD=BF,CE=CF,
∴CE=CF=$\frac{1}{2}$(AC+BC-AB),
即:r=$\frac{1}{2}$(5+12-13)=2.
故答案為:2.
點評 本題主要考查了直角三角形內切圓的性質及半徑的求法.根據已知得出CE=CF=$\frac{1}{2}$(AC+BC-AB)是解題關鍵.


科目:初中數學 來源: 題型:解答題
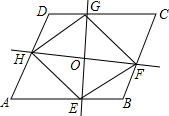 如圖,過?ABCD中對角線的中點O作兩條互相垂直的直線,分別交AB、BC、CD、DA于E、F、G、H,試判斷四邊形EFGH的形狀并說明理由.
如圖,過?ABCD中對角線的中點O作兩條互相垂直的直線,分別交AB、BC、CD、DA于E、F、G、H,試判斷四邊形EFGH的形狀并說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,Rt△ABC的斜邊AB與⊙O相切于點B,直角頂點C在⊙O上,若AC=2$\sqrt{2}$,BC=4,則⊙O的半徑是( )
如圖,Rt△ABC的斜邊AB與⊙O相切于點B,直角頂點C在⊙O上,若AC=2$\sqrt{2}$,BC=4,則⊙O的半徑是( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 我們知道,將一個立方體沿某些棱剪開,可以得到它的平面展開圖,請畫出下面立方體的一種平面展開圖,并分別把-3,-2,-1,1,2,3分別填入展開后的六個正方形內,且使原立方體相對面上的兩數和為0.
我們知道,將一個立方體沿某些棱剪開,可以得到它的平面展開圖,請畫出下面立方體的一種平面展開圖,并分別把-3,-2,-1,1,2,3分別填入展開后的六個正方形內,且使原立方體相對面上的兩數和為0.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com