
(本題滿分10分)類比、轉化、從特殊到一般等思想方法,在數學學習和研究中經常用到,如下是一個案例,請補充完整.

原題:如圖1,在□ABCD中,點E是BC邊上的中點,點F是線段AE上一點,BF的延長線交射線CD于點G,若 ,求
,求 的值.
的值.
(1)嘗試探究
在圖1中,過點E作EH∥AB交BG于點H,則AB和EH的數量關系是 ,CG和EH的數量關系是 , 的值是 .
的值是 .
(2)類比延伸
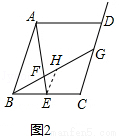
如圖2,在原題的條件下,若 則
則 的值是 (用含
的值是 (用含 的代數式表示),試寫出解答過程.
的代數式表示),試寫出解答過程.
(3)拓展遷移
如圖3,梯形ABCD中,DC∥AB,點E是BC延長線上一點,AE和BD相交于點F,若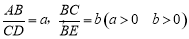 ,則
,則 的值是 (用a,b含的代數式表示).
的值是 (用a,b含的代數式表示).
(1)AB=3EH;CG=2EH;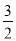 ;(2)
;(2)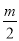 ;(3)
;(3)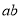 .
.
【解析】
試題分析:(1)本問體現“特殊”的情形,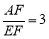 是一個確定的數值.如答圖1,過E點作平行線,構造相似三角形,利用相似三角形和中位線的性質,分別將各相關線段均統一用EH來表示,最后求得比值;
是一個確定的數值.如答圖1,過E點作平行線,構造相似三角形,利用相似三角形和中位線的性質,分別將各相關線段均統一用EH來表示,最后求得比值;
(2)本問體現“一般”的情形,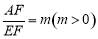 不再是一個確定的數值,但(1)問中的解題方法依然適用,如答圖2所示.
不再是一個確定的數值,但(1)問中的解題方法依然適用,如答圖2所示.
(3)本問體現“類比”與“轉化”的情形,將(1)(2)問中的解題方法推廣轉化到梯形中,如答圖3所示.
試題解析:(1)依題意,過點E作EH∥AB交BG于點H,如右圖1所示.
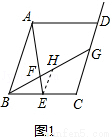
則有△ABF∽△EHF,∴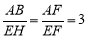 ,∴AB=3EH.
,∴AB=3EH.
∵?ABCD,EH∥AB,∴EH∥CD,
又∵E為BC中點,∴EH為△BCG的中位線,∴CG=2EH.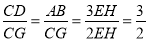 ,
,
故答案為:AB=3EH;CG=2EH; ;
;
(2)如右圖2所示,作EH∥AB交BG于點H,則△EFH∽△AFB.
∴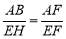 =m,∴AB=mEH.
=m,∴AB=mEH.
∵AB=CD,∴CD=mEH,∵EH∥AB∥CD,∴△BEH∽△BCG.
∴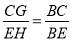 =2,∴CG=2EH,∴
=2,∴CG=2EH,∴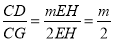 .
.
故答案為: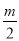 ;
;
(3)如右圖3所示,過點E作EH∥AB交BD的延長線于點H,則有EH∥AB∥CD.
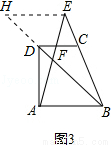
∵EH∥CD,∴△BCD∽△BEH,∴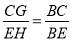 =b,∴CD=bEH.
=b,∴CD=bEH.
又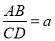 ,∴AB=aCD=abEH.
,∴AB=aCD=abEH.
∵EH∥AB,∴△ABF∽△EHF,∴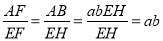 ,
,
故答案為: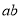 .
.
考點:1.相似形綜合題;2.平行四邊形的性質;3.梯形;4.相似三角形的判定與性質.


科目:初中數學 來源:2014-2015學年江蘇省江陰市長涇片八年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖:等腰直角△ABC中,若∠ACB=90°,CD=DE=CE,則∠DAB的度數為( )

A、60° B、30° C、45° D、15°
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省蘇州市高新區九年級上學期期中聯考數學試卷(解析版) 題型:選擇題
已知矩形ABCD中,AB=1,在BC上取一點E,沿AE將△ABE向上折疊,使B點落在AD上的F點,若四邊形ECDF與矩形ABCD相似,則AD=( )

A. B.
B. C.
C. D.2
D.2
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省江陰市青陽片九年級上學期期中考試數學試卷(解析版) 題型:解答題
(本題滿分6分)在等腰△ABC中,三邊分別為a、b、c,其中 ,若關于x的方程
,若關于x的方程 有兩個相等的實數根,求△ABC的周長.
有兩個相等的實數根,求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省泰興市七年級上學期期中考試數學試卷(解析版) 題型:選擇題
下列軸對稱圖形中,可以用沒有刻度的直尺畫出對稱軸的有( )

A.1個 B.2個 C.3個 D,4個
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省江陰市青陽片七年級上學期期中考試數學試卷 題型:解答題
(本題11分)探索性問題:
已知: 是最小的正整數,且
是最小的正整數,且 滿足
滿足 .
.
(1)請求出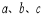 的值;
的值;
(2) 所對應的點分別為A、B、C,點P為動點,其對應的數為x,點P在0到2之間運動時(即
所對應的點分別為A、B、C,點P為動點,其對應的數為x,點P在0到2之間運動時(即 時),請化簡式子:
時),請化簡式子: ;(寫出化簡過程)
;(寫出化簡過程)
(3)在(1)、(2)的條件下,點A、B、C開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和5個單位長度的速度向右運動,假設 秒鐘過后,若點B與點C之間的距離表示為BC,點A與點B之間的距離表示為AB.請問:BC-AB的值是否隨著時間t的變化而改變?若變化,請說明理由;若不變,請求其值.
秒鐘過后,若點B與點C之間的距離表示為BC,點A與點B之間的距離表示為AB.請問:BC-AB的值是否隨著時間t的變化而改變?若變化,請說明理由;若不變,請求其值.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省泰州市姜堰區八年級上學期期中考試數學試卷(解析版) 題型:填空題
一個直角三角形的兩條直角邊長分別為5、12,則斜邊上的中線長為 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省附中八年級上學期期中考試數學試卷(解析版) 題型:解答題
(本題滿分10分)如圖所示,△ACB與△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,點D為AB邊上的一點,若AB=17,BD=12,
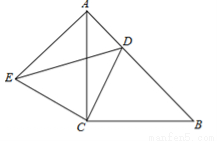
(1)求證:△BCD≌△ACE;
(2)求DE的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com