Question

1．如圖，直線y=$\frac{1}{2}$x+2分別交x、y軸于點A、C，點P是該直線與反比例函數y=$\frac{k}{x}$在第一象限內的交點，PB⊥x軸，B為垂足，S_△ABP=9．
（1）直接寫出點A的坐標（-4，0）；點C的坐標（0，2）；點P的坐標（2，3）；
（2）若Q為反比例函數在第一象限圖象上的點（點Q與點P不重合），且Q點的橫坐標為6，在x軸上確定一點M，使MP+MQ最小，并直接寫出點M的坐標；
（3）設點R與點P在同一個反比例函數的圖象上，且點R在直線PB的右側，作RT⊥x軸，T為垂足，當△BRT與△AOC相似時，求點R的坐標．

Answer 1

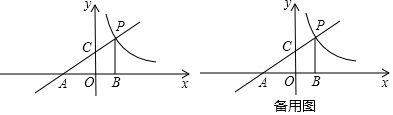
分析 （1）利用待定系數法可以求出點A、C的坐標，由△ACO∽△APB，推出$\frac{OA}{AB}$=$\frac{OC}{PB}$=$\frac{2}{3}$，推出OB=2，PB=3，由此即可解決問題．
（2）如圖1中，作點P關于x軸的對稱點P′，連接QP′與x軸交于點M，LJ PM，此時PM+MQ的值最小．求出直線P′Q的解析式即可．
（3）設R點的坐標為（m，$\frac{6}{m}$），分兩種情形分別利用相似三角形的性質，列出方程解決問題．

解答 解：（1）∵直線y=$\frac{1}{2}$x+2分別交x、y軸于點A、C，
∴A點坐標（-4，0），C點坐標（0，2），
∵S_△AOC=$\frac{1}{2}$×4×2=4，
∵OC∥PB，S_△ABP=9，
∴△ACO∽△APB，
∴$\frac{OA}{AB}$=$\frac{OC}{PB}$=$\frac{2}{3}$，
∴AB=6，PB=3，
∴OB=2，
∴P（2，3）
故答案為（-4，0），（0，2），（2，3）．

（2）如圖1中，作點P關于x軸的對稱點P′，連接QP′與x軸交于點M，LJ PM，此時PM+MQ的值最小．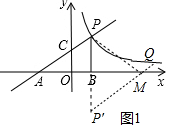

∵點P（2，3）在，反比例函數y=$\frac{k}{x}$上，
∴k=6，
∴Q（6，1），P′（2，-3），
∴直線P′Q是解析式為y=x-5，
令y=0，得x=5，
∴M（5，0）．

（3）如圖2中，設R點的坐標為（m，$\frac{6}{m}$），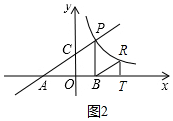

∵P點坐標為（2，3），
又∵△BRT∽△ACO，
∴$\frac{OA}{BT}$=$\frac{CO}{RT}$，
∴$\frac{4}{m-2}$=$\frac{2}{\frac{6}{m}}$，
解得m₁=1+$\sqrt{13}$，m₂=1-$\sqrt{13}$（舍去），
∴R（1+$\sqrt{13}$，$\frac{\sqrt{13}-1}{2}$），
②如圖3中，△BRT∽△CAO時，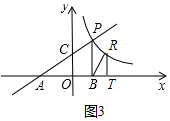

∴$\frac{OA}{RT}$=$\frac{OC}{BT}$時，
∴$\frac{4}{\frac{6}{m}}$=$\frac{2}{m-2}$，
解得m₁=3，m₂=-1（舍去）
∴R（3，2）
綜上所述，滿足條件的點R坐標為（1+$\sqrt{13}$，$\frac{\sqrt{13}-1}{2}$）或（3，2）．

點評 本題考查反比例函數綜合題、相似三角形的判定和性質、軸對稱-最短問題等知識，解題的關鍵是靈活運用所學知識，學會利用參數解決問題，學會用方程的思想思考問題，屬于中考常考題型．