
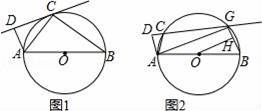
如圖1,AB為⊙O的直徑,C為⊙O上一點,作AD⊥CD,垂足為D.
(1)若直線CD與⊙O相切于點C,求證:△ADC∽△ACB;
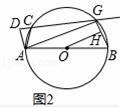
(2)如果把直線CD向下平行移動,如圖2,直線CD交⊙O于C、G兩點,若題目中的其他條件不變,tan∠DAC=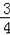
 ,AB=10,求圓心O到GB的距離OH的長.
,AB=10,求圓心O到GB的距離OH的長.

【考點】切線的性質;相似三角形的判定與性質.
【分析】(1)首先連接OC,由CD切⊙O于C,根據切線的性質,可得OC⊥CD,又由AD⊥CD,可得OC∥AD,又由OA=OC,易證得∠DAC=∠CAO,根據圓周角定理求得∠ACB=90°,得出∠ADC=∠ACB,即可證得結論;
(2)由于四邊形ABGC為⊙O的內接四邊形,根據圓的內接四邊形的性質得∠B+∠ACG=180°,易得∠ACD=∠B,又∠ADC=∠AGB=90°,利用等角的余角相等得到∠DAC=∠GAB,根據tan∠DAC=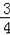
 =tan∠GAB=
=tan∠GAB=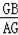
 和勾股定理求得AG=8,GB=6,然后求得△ABG∽△OBH,根據相似三角形的性質求得
和勾股定理求得AG=8,GB=6,然后求得△ABG∽△OBH,根據相似三角形的性質求得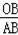
 =
=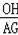
 =
=
 ,即可求得OH=4.
,即可求得OH=4.
【解答】(1)證明:連接OC,如圖1,
∵直線CD與⊙O相切于點C,
∴OC⊥CD,
∵AD⊥CD,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
∵AB為⊙O的直徑,
∴∠ACB=90°,
∴∠ADC=∠ACB,
∴△ADC∽△ACB;
(2)解:如圖2,∵AB是⊙O的直徑,
∴∠AGB=90°,
∵四邊形ABGC是⊙O的內接四邊形,
∴∠ACD=∠B,
∵∠ADC=∠AGB=90°,
∴∠DAC=∠GAB,
∵tan∠DAC=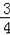
 =tan∠GAB=
=tan∠GAB=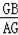
 ,
,
設GB=3x,AG=4x,
∵AB=10,
∴(3x)2+(4x)2=102,
解得x=2,
∴AG=8,GB=6,
∵OH⊥GB,AG⊥GB,
∴OH∥AG,
∴△ABG∽△OBH,
∴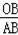
 =
=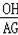
 =
=
 ,
,
∴OH=4.



【點評】此題考查了切線的性質、垂徑定理、等腰三角形的性質、平行線的判定與性質以及相似三角形的判定與性質.此題難度適中,注意掌握輔助線的作法,注意數形結合思想的應用.


科目:初中數學 來源: 題型:
體育課上,小明、小強、小華三人在學習訓練踢足球,足球從一人傳到另一人就記為踢一次.
(1)如果從小強開始踢,經過兩次踢后,足球踢到了小華處的概率是多少(用樹狀圖表示或列表說明);
(2)如果踢三次后,球踢到了小明處的可能性最小,應從誰開始踢?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
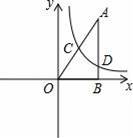
如圖,Rt△ABO在直角坐標系中,AB⊥x軸于點B,AO=10,sin∠AOB=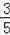
 ,反比例函數y=
,反比例函數y=
 (x>0)的圖象經過AO的中點C,且與AB交于點D,則BD= .
(x>0)的圖象經過AO的中點C,且與AB交于點D,則BD= .

查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,△ABC中,∠ACB=90°,∠A=30°,AB=16.點P是斜邊AB
上一點.過點P作PQ⊥AB,垂足為P,交邊AC(或邊CB)于點Q,
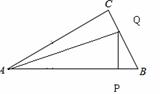 設AP=x,△APQ的面積為y,則y與x之間的函數圖象大致為( )
設AP=x,△APQ的面積為y,則y與x之間的函數圖象大致為( )
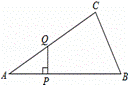
① ②
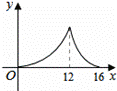
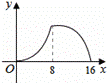
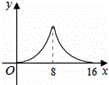
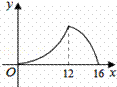
A、 B 、 C、 D、
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com