
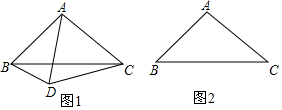
分析 (1)由∠BAC=100°,AB=AC,可以確定∠ABC=∠ACB=40°,旋轉角為α,α=60°時△ACD是等邊三角形,且AC=AD=AB=CD,知道∠BAD的度數,進而求得∠CBD的大小;
(2)根據旋轉的定義即可得.
(3)結合(1)(2)的解題過程可以發現規律,△ACD是等邊三角形時,CD在△ABC內部時,CD在△ABC外部時,求得答案
解答 解:(1)∵∠BAC=100°,AB=AC,
∴∠ABC=∠ACB=40°,當α=60°時,
由旋轉的性質得AC=CD,
∴△ACD是等邊三角形,
∴∠DAC=60°,
∴∠BAD=∠BAC-∠DAC=100°-60°=40°,
∵AB=AC,AD=AC,
∴∠ABD=∠ADB=$\frac{180°-∠BAD}{2}$=70°,
∴∠CBD=∠ABD-∠ABC=70°-40°=30°,
故答案為:30°;
(2)如圖2所示;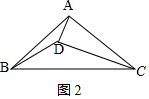
(3)①由(1)可知,∠α=60°時可得∠BAD=100°-60°=40°,∠ABC=∠ACB=90°-$\frac{100°}{2}$=40°,
∠ABD=90°-$\frac{1}{2}$∠BAD=120°-$\frac{100°}{2}$=70°,
∠CBD=∠ABD-∠ABC=30°.
②如圖3,翻折△BDC到△BD1C,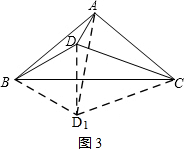
則此時∠CBD1=30°,
∠BCD=60°-∠ACB=$\frac{100°}{2}$-30°=20°,
∠α=∠ACB-∠BCD1=∠ACB-∠BCD=$\frac{180°-100°}{2}$-20°=20°;
③以C為圓心CD為半徑畫圓弧交BD的延長線于點D2,連接CD2,
∠CDD2=∠CBD+∠BCD=30°+$\frac{100°}{2}$-30°=50°,
∠DCD2=180°-2∠CDD2=180°-100°=80°,
∠α=60°+∠DCD2=140°.
綜上所述,α為60°或20°或140°時,∠CBD=30°.
點評 本題考查旋轉變換的定義及性質、等腰三角形的性質,解答這類題目的關鍵是要善于從探究特殊結論中歸納出一般性解題方法,并靈活運用這種方法解答一般性的問題,真正達到舉一反三的目的.


 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
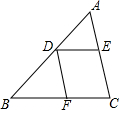 如圖,在△ABC中,D是AB邊上一點,DE∥BC,DF∥AC,下列結論正確的是( )
如圖,在△ABC中,D是AB邊上一點,DE∥BC,DF∥AC,下列結論正確的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{AC}$ | B. | $\frac{DE}{BF}$=$\frac{AE}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{BD}$=$\frac{DF}{AC}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
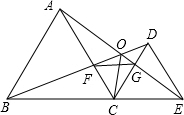 如圖,已知△ABC和△DCE均是等邊三角形,點B、C、E在同一條直線上,AE與BD交于點O,AE與CD交于點G,AC與BD交于點F,連接OC、FG,則下列結論:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正確的結論有( )個.
如圖,已知△ABC和△DCE均是等邊三角形,點B、C、E在同一條直線上,AE與BD交于點O,AE與CD交于點G,AC與BD交于點F,連接OC、FG,則下列結論:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正確的結論有( )個.| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com