
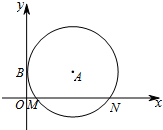
 如圖,在平面直角坐標系xOy中,⊙A與y軸相切于點B(0,$\frac{3}{2}$),與x軸相交于M、N兩點.如果點M的坐標為($\frac{1}{2}$,0),求⊙A的半徑及點N的坐標.
如圖,在平面直角坐標系xOy中,⊙A與y軸相切于點B(0,$\frac{3}{2}$),與x軸相交于M、N兩點.如果點M的坐標為($\frac{1}{2}$,0),求⊙A的半徑及點N的坐標. 分析 連接AB、AM、過A作AC⊥MN于C,設⊙A的半徑是R,由切線的性質得出AB⊥y軸,由題意得出AB=AM=R,CM=R-$\frac{1}{2}$,AC=$\frac{3}{2}$,MN=2CM,由勾股定理得出方程,解方程求出R,得出CM,得出ON的長即可.
解答 解: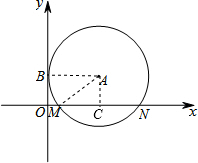 連接AB、AM、過A作AC⊥MN于C,如圖所示:
連接AB、AM、過A作AC⊥MN于C,如圖所示:
設⊙A的半徑是R,
∵⊙A與y軸相切于B,
∴AB⊥y軸,
∵點B(0,$\frac{3}{2}$),與x軸相交于M、N兩點,點M的坐標為($\frac{1}{2}$,0),
∴AB=AM=R,CM=R-$\frac{1}{2}$,AC=$\frac{3}{2}$,MN=2CM,
由勾股定理得:R2=(R-$\frac{1}{2}$)2+($\frac{3}{2}$)2,
解得:R=2.5,即⊙A的半徑為2.5;
∴CM=CN=2.5-$\frac{1}{2}$=2,
∴ON=$\frac{1}{2}$+2+2=4$\frac{1}{2}$,
即N的坐標是(4$\frac{1}{2}$,0).
點評 本題考查了切線的性質、坐標與圖形性質、勾股定理;熟練掌握切線的性質,由勾股定理得出方程求出半徑是解決問題的關鍵.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
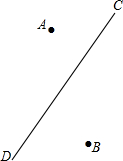 一輛貨車在公路(直線CD)上由點C向點D方向行駛,村莊A、B分別位于道路CD的兩側,司機師傅要在公路上選擇一個貨物的下貨點.
一輛貨車在公路(直線CD)上由點C向點D方向行駛,村莊A、B分別位于道路CD的兩側,司機師傅要在公路上選擇一個貨物的下貨點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com