
分析 (1)待定系數法求解可得;
(2)若要使點B、B′、C、C′為頂點的四邊形為菱形,則拋物線可以沿左右方向或上下方向平移BC的長度,據此分別求出兩種情況下菱形的面積,可知平移的方向和距離,繼而可得答案.
解答 解:(1)把點A(-3,0),B(2,0)代入y=x2+bx+c得:$\left\{\begin{array}{l}{9-3b+c=0}\\{4+2b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=1}\\{c=-6}\end{array}\right.$,
∴拋物線的解析式為y=x2+x-6;
(2)∵OB=2,OC=6,
∴BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=2$\sqrt{10}$,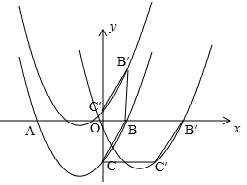
若將拋物線向左或向右平移2$\sqrt{10}$個單位時,菱形的面積為2$\sqrt{10}$×6=12$\sqrt{10}$;
若將拋物線向上或向下平移2$\sqrt{10}$個單位,菱形的面積為2$\sqrt{10}$×2=4$\sqrt{10}$,
∴當以點B、B′、C、C′為頂點的菱形面積最大時,應將拋物線向左或向右平移2$\sqrt{10}$個單位,
向左平移時拋物線C1的解析式為y=(x+2$\sqrt{10}$)2+x+2$\sqrt{10}$-6=x2+(4$\sqrt{10}$+1)x+34+2$\sqrt{10}$,
向右平移時拋物線C1的解析式為y=(x-2$\sqrt{10}$)2+x-2$\sqrt{10}$-6=x2-(4$\sqrt{10}$-1)x+34-2$\sqrt{10}$.
點評 本題主要考查待定系數法求二次函數的解析式及菱形的性質,熟練掌握菱形的性質及二次函數的圖象與幾何變換是解題的關鍵.


科目:初中數學 來源: 題型:填空題
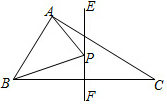 如圖,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,點P為直線EF上的任一點,則△ABP周長的最小值是7.
如圖,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,點P為直線EF上的任一點,則△ABP周長的最小值是7.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
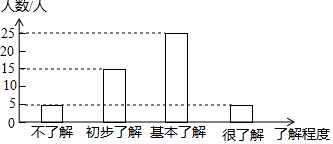 大同中學德育處針對同學們對廈門地鐵建設情況的了解程度進行隨機抽樣調查,并制成如下統計圖,請根據圖中的信息,解答下列問題:
大同中學德育處針對同學們對廈門地鐵建設情況的了解程度進行隨機抽樣調查,并制成如下統計圖,請根據圖中的信息,解答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,AD為∠BAC的平分線,DE⊥AB于點E,DF⊥AC于點F,△ABC面積是27cm2,AB=10cm,AC=8cm.
如圖,在△ABC中,AD為∠BAC的平分線,DE⊥AB于點E,DF⊥AC于點F,△ABC面積是27cm2,AB=10cm,AC=8cm.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
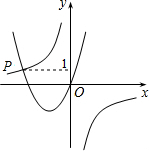 已知函數y=$\frac{-2}{x}$與y=ax2-bx(a>0,b<0)的圖象交于點P,點P的縱坐標為1.則關于x的不等式ax2+$\frac{2}{x}$>bx的解是x<-2或x>0.
已知函數y=$\frac{-2}{x}$與y=ax2-bx(a>0,b<0)的圖象交于點P,點P的縱坐標為1.則關于x的不等式ax2+$\frac{2}{x}$>bx的解是x<-2或x>0.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com