
分析 如圖,AF∥DC,EF∥BC,DE∥AB,可知AD、BE、CF都是直徑,推出DE=AB,EF=BC,FA=CD,設CD=x,AB=x-d,則BC=x+d,EF=x+d,由題意2(x-d)2+2x2+2(x+d)2=2008,整理得3x2+2d2=1004,利用不等式,求出x的整數解,即可解決問題.
解答 解:如圖,AF∥DC,EF∥BC,DE∥AB,可知AD、BE、CF都是直徑,
∴DE=AB,EF=BC,FA=CD,設CD=x,AB=x-d,則BC=x+d,EF=x+d,
由題意2(x-d)2+2x2+2(x+d)2=2008,整理得3x2+2d2=1004,
顯然,x2=$\frac{1004-2p9vv5xb5^{2}}{3}$<335,得x≤18,
又d2=$\frac{1004-3{x}^{2}}{2}$<x2,得到5x2>1004,
∴x2>200,可得x≥15,
∵x是偶數,
∴x=16或18,
若x=16,則d2=$\frac{1004-3{x}^{2}}{2}$=118,顯然無整數解,
若x=18,則d2=$\frac{1004-3{x}^{2}}{2}$=16,
∵d>0,
∴d=4,
∴AB=x-d=14,CD=x=18,BC=x+d=22,
∴AB+BC+CD+DE+EF+FA=2(14+18+22)=108.
點評 本題考查正多邊形與圓、二元二次方方程的整數解問題、不等式等整數,解題的關鍵是學會構建二元二次方程,學會利用不等式確定整數解,題目比較難,屬于競賽題目.


 智慧小復習系列答案
智慧小復習系列答案科目:初中數學 來源: 題型:選擇題
| A. | ∠α的補角和∠β的補角相等 | B. | ∠α的余角和∠β的補角相等 | ||
| C. | ∠α的余角和∠β的補角互余 | D. | ∠α的余角和∠β的補角互補 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
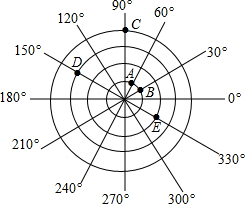 如圖,是一臺雷達探測器在點O處測得的結果,圖中顯示,在A、B、C,D,E處有目標出現,試用適當方式分別表示每個目標的位置,哪處出現的目標到探測點的距離最遠?
如圖,是一臺雷達探測器在點O處測得的結果,圖中顯示,在A、B、C,D,E處有目標出現,試用適當方式分別表示每個目標的位置,哪處出現的目標到探測點的距離最遠?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知△ABC在平面直角坐標系中的位置如圖所示.
已知△ABC在平面直角坐標系中的位置如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
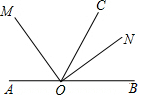 如圖,點O是直線AB上一點,OM平分∠AOC,ON平分∠BOC.
如圖,點O是直線AB上一點,OM平分∠AOC,ON平分∠BOC.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com