
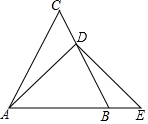
 如圖,等邊△ABC中,點D在邊BC上,點E在AB的延長線上,且BE=CD,試問:線段DE與AD相等嗎?并說明理由.
如圖,等邊△ABC中,點D在邊BC上,點E在AB的延長線上,且BE=CD,試問:線段DE與AD相等嗎?并說明理由. 分析 過點D作DF∥AC,交AB于點F,證明△AFD≌△DBE即可.
解答 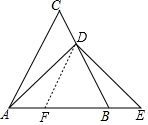 解:DE=AD,
解:DE=AD,
理由如下:
如圖,過點D作DF∥AC,交AB于點F,
∵△ABC為等邊三角形,
∴△BFD為等邊三角形,
∴BD=BF,且AB=BC,
∴AF=CD=BE,
∵∠DFB=∠DBF=60°,
∴∠AFD=∠DBE=120°,
在△AFD和△DBE中
$\left\{\begin{array}{l}{AF=BE}\\{∠AFD=∠EBD}\\{DF=DB}\end{array}\right.$
∴△AFD≌△DBE(SAS),
∴DE=AD.
點評 本題主要考查全等三角形的判定和性質及等邊三角形的性質,由條件構造全等三角形是解題的關鍵.


 靈星計算小達人系列答案
靈星計算小達人系列答案科目:初中數學 來源: 題型:解答題
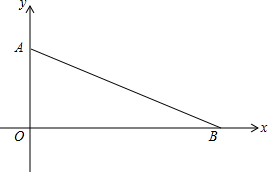 如圖,在平面直角坐標系中,點A(0,7),B(24,0).△AOB內是否有一點P到各邊的距離相等?如果有,請作出這一點,并求出符合條件的點P的坐標.
如圖,在平面直角坐標系中,點A(0,7),B(24,0).△AOB內是否有一點P到各邊的距離相等?如果有,請作出這一點,并求出符合條件的點P的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
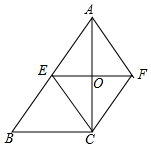 如圖,在四邊形ABCF中,∠ACB=90°,點E是AB邊的中點,點F恰是點E關于AC所在直線的對稱點.
如圖,在四邊形ABCF中,∠ACB=90°,點E是AB邊的中點,點F恰是點E關于AC所在直線的對稱點.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 按要求畫圖并填空:如圖AD∥BC,AB∥CD,
按要求畫圖并填空:如圖AD∥BC,AB∥CD,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com