
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
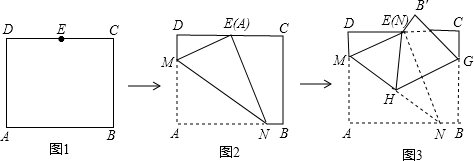
分析 根據(jù)折疊的性質(zhì)可得EM∥GH,再根據(jù)等量代換,即可得出∠AMN=∠EHG;在直角三角形中運用勾股定理,即可得出AM=EM=7.4,再根據(jù)相似三角形的性質(zhì),即可得出EN=$\frac{37}{6}\sqrt{3}$=AN,進而得到tan∠AMN=$\frac{AN}{MN}$=$\frac{5}{6}\sqrt{3}$=tan∠EHG,最后根據(jù)∠EMH≠60°,可得△MEH不是等邊三角形.
解答 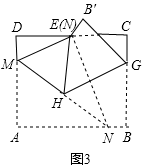 解:如圖3,由折疊可得,∠MEN=∠A=90°,HG⊥NE,
解:如圖3,由折疊可得,∠MEN=∠A=90°,HG⊥NE,
即ME⊥EN,HG⊥EN,
∴EM∥GH,故①正確;
∴∠NME=∠NHG,
由折疊可得,∠NME=∠AMN,∠EHG=∠NHG,
∴∠AMN=∠EHG,故③正確;
如圖2,作NF⊥CD于F.
設(shè)DM=x,則AM=EM=10-x,
∵點E是CD的中點,AB=CD=8$\sqrt{3}$,
∴DE=$\frac{1}{2}$CD=4$\sqrt{3}$,
在Rt△DEM中,∵DM2+DE2=EM2,
∴(4$\sqrt{3}$)2+x2=(10-x)2,
解得x=2.6,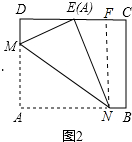
∴DM=2.6,AM=EM=7.4,
∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,
∴∠DEM=∠ENF,
∵∠D=∠EFN=90°,
∴△DME∽△FEN,
∴$\frac{DE}{FN}$=$\frac{EM}{EN}$,即$\frac{4\sqrt{3}}{10}$=$\frac{7.4}{EN}$,
∴EN=$\frac{37}{6}\sqrt{3}$,
∴AN=$\frac{37}{6}\sqrt{3}$,
∴tan∠AMN=$\frac{AN}{MN}$=$\frac{5}{6}\sqrt{3}$,
∴tan∠EHG=$\frac{5\sqrt{3}}{6}$,故④正確;
又∵tan60°=$\sqrt{3}$>$\frac{5}{6}\sqrt{3}$,
∴∠AMN≠60°,即∠EMH≠60°,
∴△MEH不是等邊三角形,故②錯誤.
∴正確的結(jié)論有3個.
故選:C.
點評 本題屬于四邊形綜合題,主要考查翻折變換、勾股定理、相似三角形的判定和性質(zhì)等知識的綜合應(yīng)用,解題的關(guān)鍵是作輔助線構(gòu)造相似三角形,依據(jù)相似三角形對應(yīng)邊成比例,求得EN的長度.解決折疊問題時,常常設(shè)要求的線段長為x,然后根據(jù)折疊和軸對稱的性質(zhì)用含x的代數(shù)式表示其他線段的長度,選擇適當?shù)闹苯侨切危\用勾股定理列出方程求出答案.


 培優(yōu)好卷單元加期末卷系列答案
培優(yōu)好卷單元加期末卷系列答案 一線名師權(quán)威作業(yè)本系列答案
一線名師權(quán)威作業(yè)本系列答案科目:初中數(shù)學 來源: 題型:填空題
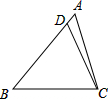 在△ABC中,D為AB邊上一點,且∠BCD=∠A,已知BC=2$\sqrt{2}$,AB=3,則AD=$\frac{1}{3}$.
在△ABC中,D為AB邊上一點,且∠BCD=∠A,已知BC=2$\sqrt{2}$,AB=3,則AD=$\frac{1}{3}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
 如圖,下列結(jié)論正確的個數(shù)是( )
如圖,下列結(jié)論正確的個數(shù)是( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 0.612×107 | B. | 6.12×106 | C. | 61.2×105 | D. | 612×106 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 調(diào)查2017年2月份利辛市場上某品牌飲料的質(zhì)量 | |
| B. | 調(diào)查某月份長江安徽段水域的水質(zhì)量情況 | |
| C. | 光明節(jié)能廠檢測一批新型節(jié)能燈的使用壽命 | |
| D. | 了解某班50名學生的年齡情況 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\frac{x-2}{{x}^{2}-3x+2}$ | B. | $\frac{1}{x-2}$ | C. | $\frac{2x-4}{x-1}$ | D. | $\frac{x+2}{x+1}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com