
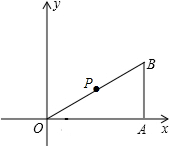
 己知:Rt△OAB在直角坐標系中的位置如圖所示,點B的坐標為(4,2),P為OB的中點,點C為折線OAB上的動點,線段PC把Rt△OAB分割成兩部分,問:點C在什么位置時,分割得到的三角形與Rt△OAB相似?要求在圖上畫出所有符合要求的線段PC,并求出相應的點C的坐標.
己知:Rt△OAB在直角坐標系中的位置如圖所示,點B的坐標為(4,2),P為OB的中點,點C為折線OAB上的動點,線段PC把Rt△OAB分割成兩部分,問:點C在什么位置時,分割得到的三角形與Rt△OAB相似?要求在圖上畫出所有符合要求的線段PC,并求出相應的點C的坐標. 分析 由于C點不確定,故分△OPC∽△OBA,△BPC∽△BOA,△OPC∽△OAB三種情況進行討論.
解答 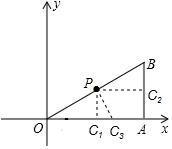 解:∵點B的坐標為(4,2),
解:∵點B的坐標為(4,2),
∴OA=4,AB=2,OB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,OP=$\sqrt{5}$.
如圖,當△OPC∽△OBA時,
∵$\frac{OC}{OA}$=$\frac{OP}{OB}$=$\frac{1}{2}$,即$\frac{PC}{2}$=$\frac{OC}{4}$=$\frac{1}{2}$,
∴PC=1,OC=2,
∴C1(2,0);
當△BPC∽△BOA時,
∵$\frac{PB}{OB}$=$\frac{BC}{OA}$=$\frac{PC}{OA}$,即$\frac{1}{2}$=$\frac{BC}{2}$=$\frac{PC}{4}$,解得BC=2,
∴AC=1-1=1,
∴C2(4,1);
當△OPC∽△OAB時,
∴$\frac{OP}{OA}$=$\frac{OC}{OB}$,即$\frac{\sqrt{5}}{4}$=$\frac{OC}{2\sqrt{5}}$,解得OC=2.5,
∴C3(2.5,0);
綜上所述,C點坐標為:(2,0)或(4,1)或(2.5,0).
點評 本題考查的是相似三角形的判定,在解答此題時要注意進行分類討論,不要漏解.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{15}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | 14 | B. | 7 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在正方形ABCD中,點M是BC邊上任意一點,請你僅用無刻度直尺,用連線的方法,在圖中按要求作圖(保留作圖痕跡,不寫作法),在AB邊上求一點N,連接CN,使CN=AM,并說明理由.
如圖,在正方形ABCD中,點M是BC邊上任意一點,請你僅用無刻度直尺,用連線的方法,在圖中按要求作圖(保留作圖痕跡,不寫作法),在AB邊上求一點N,連接CN,使CN=AM,并說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com