
 如圖,在正方形ABCD中,點M是BC邊上任意一點,請你僅用無刻度直尺,用連線的方法,在圖中按要求作圖(保留作圖痕跡,不寫作法),在AB邊上求一點N,連接CN,使CN=AM,并說明理由.
如圖,在正方形ABCD中,點M是BC邊上任意一點,請你僅用無刻度直尺,用連線的方法,在圖中按要求作圖(保留作圖痕跡,不寫作法),在AB邊上求一點N,連接CN,使CN=AM,并說明理由. 分析 連接BD,BD與AM交于點O,連接CO并延長交于AB,則CO與AB的交點為點N.可先證明△AOD≌△COD,再證明△ABM≌△CBN,故可得出CN=AM.
解答 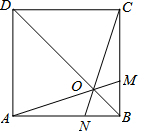 解:如圖,連接BD,BD與AM交于點O,連接CO并延長交于AB,則CO與AB的交點為點N,則CN為所作.
解:如圖,連接BD,BD與AM交于點O,連接CO并延長交于AB,則CO與AB的交點為點N,則CN為所作.
理由:在△AOD與△COD中,
∵$\left\{\begin{array}{l}{AD=CD}\\{∠ADO=∠CDO}\\{OD=OD}\end{array}\right.$,
∴△AOD≌△COD(SAS),
∴∠OAD=∠OCD,
∴∠BAM=∠BCN.
在△ABM與△CBN中,
∵$\left\{\begin{array}{l}{∠BAM=∠BCN}\\{AB=CB}\\{∠ABM=∠CBN}\end{array}\right.$,
∴△ABM≌△CBN(ASA),
∴CN=AM.
點評 本題考查了作圖-基本作圖,解決此題的關鍵是利用正方形的性質求解.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:選擇題
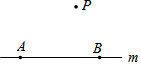 如圖,點A,B在直線m上,點P在直線m外,點Q是直線m上異于點A,B的任意一點,則下列說法或結論正確的是( )
如圖,點A,B在直線m上,點P在直線m外,點Q是直線m上異于點A,B的任意一點,則下列說法或結論正確的是( )| A. | 射線AB和射線BA表示同一條射線 | |
| B. | 線段PQ的長度就是點P到直線m的距離 | |
| C. | 連接AP,BP,則AP+BP>AB | |
| D. | 不論點Q在何處,AQ=AB-BQ或AQ=AB+BQ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y2<y3<y1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
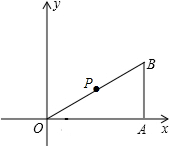 己知:Rt△OAB在直角坐標系中的位置如圖所示,點B的坐標為(4,2),P為OB的中點,點C為折線OAB上的動點,線段PC把Rt△OAB分割成兩部分,問:點C在什么位置時,分割得到的三角形與Rt△OAB相似?要求在圖上畫出所有符合要求的線段PC,并求出相應的點C的坐標.
己知:Rt△OAB在直角坐標系中的位置如圖所示,點B的坐標為(4,2),P為OB的中點,點C為折線OAB上的動點,線段PC把Rt△OAB分割成兩部分,問:點C在什么位置時,分割得到的三角形與Rt△OAB相似?要求在圖上畫出所有符合要求的線段PC,并求出相應的點C的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
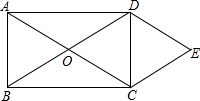 如圖,O為矩形ABCD對角線的交點,DE∥AC,CE∥BD.
如圖,O為矩形ABCD對角線的交點,DE∥AC,CE∥BD.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com