
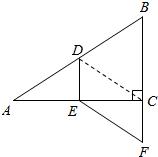
 如圖,在Rt△ABC中,∠ACB=90°,點D,E分別是邊AB,AC的中點,延長BC至F,使CF=$\frac{1}{2}$BC,若AB=10,則EF的長是( )
如圖,在Rt△ABC中,∠ACB=90°,點D,E分別是邊AB,AC的中點,延長BC至F,使CF=$\frac{1}{2}$BC,若AB=10,則EF的長是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 由三角形中位線定理得出DE∥BC,由直角三角形斜邊上的中線性質得出CD=$\frac{1}{2}$AB=AD=BD,又CF=$\frac{1}{2}$BC,即可證出四邊形CDEF是平行四邊形,由此即可解決問題.
解答  解:∵AD=DB,AE=EC,
解:∵AD=DB,AE=EC,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∵CF=$\frac{1}{2}$BC,
∴DF∥CF,DF=CF,
∴四邊形DEFC是平行四邊形,
∴EF=CD,
∵∠ACB=90°,AD=DB,AB=10,
∴CD=$\frac{1}{2}$AB=5,
∴EF=5.
故選A.
點評 本題考查了直角三角形斜邊上的中線等于斜邊的一半的性質,等腰三角形的性質,全等三角形的判定與性質,熟記各性質并確定出全等三角形是解題的關鍵.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源:2016-2017學年四川省成都市金堂縣八年級上學期期末考試數學試卷就(解析版) 題型:填空題
已知:m、n為兩個連續的整數,且m<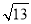 <n,則mn的平方根 =__.
<n,則mn的平方根 =__.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知△ABC的三個頂點的坐標分別為:A(-2,3)、B(-6,0)、C(-1,0).
如圖,已知△ABC的三個頂點的坐標分別為:A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com