
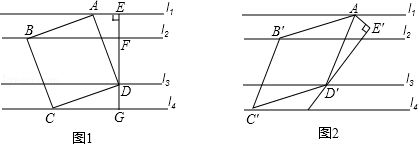
分析 (1)利用已知得出△AED≌△DGC(AAS),即可得出AE,以及正方形的邊長;
(2)如圖2過點B作BE⊥L1于點E,反向延長BE交L4于點F,則BE=1,BF=3,由四邊形ABCD是矩形,∠ABC=90°,∠ABE+∠FBC=90°,根據∠ABE+∠EAB=90°,得到∠FBC=∠EAB,然后分類討論,求得矩形的寬.
(3)首先過點E′作ON垂直于l1分別交l1,l2于點O,N,∠AEO=30°,則∠ED′N=60°,可求出AE=1,EO,EN,ED′的長,進而由勾股定理可知菱形的邊長.
解答 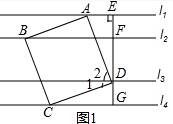 解:(1)∵l1∥l2∥l3∥l4,∠AED=90°
解:(1)∵l1∥l2∥l3∥l4,∠AED=90°
∴∠DGC=90°,
∵四邊形ABCD為正方形
∴∠ADC=90°,AD=CD,∵∠ADE+∠2=90°,
∴∠1+∠2=90°,
∴∠1=∠ADE,
∵l3∥l4
∴∠1=∠DCG,
∠ADE=∠DCG,
在△AED與△DGC中,
$\left\{\begin{array}{l}{∠ADE=∠DCG}\\{∠AED=∠GDC}\\{AD=CD}\end{array}\right.$,
∴△AED≌△GDC(AAS),
∴AE=GD=1,ED=GC=3,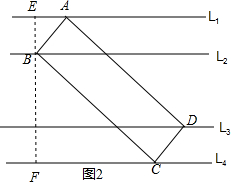 ∴AD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴AD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
故答案為:$\sqrt{10}$;
(2)如圖2過點B作BE⊥L1于點E,反向延長BE交L4于點F,
則BE=1,BF=3,
∵四邊形ABCD是矩形,
∴∠ABC=90°,
∴∠ABE+∠FBC=90°,
∵∠ABE+∠EAB=90°,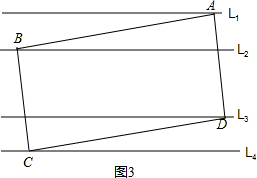 ∴∠FBC=∠EAB,
∴∠FBC=∠EAB,
當AB<BC時,AB=$\frac{1}{2}$BC,
∴AE=$\frac{1}{2}$BF=$\frac{3}{2}$,
∴AB=$\sqrt{{1}^{2}+(\frac{3}{2})^{2}}$=$\frac{\sqrt{13}}{2}$;
如圖3當AB>BC時,
同理可得:BC=$\frac{\sqrt{37}}{2}$,
∴矩形的寬為:$\frac{\sqrt{13}}{2}$,$\frac{\sqrt{37}}{2}$;
(3)如圖4過點E′作ON垂直于l1分別交l1,l4于點O,N,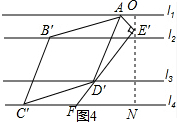
∵∠OAE′=30°,則∠E′FN=60°
∵AE′=AE=1,
故E′O=$\frac{1}{2}$,E′N=$\frac{5}{2}$,E′D′=$\frac{5\sqrt{3}}{3}$,
由勾股定理可知菱形的邊長為:$\sqrt{\frac{25}{3}+1}$=$\frac{\sqrt{84}}{3}$=$\frac{2\sqrt{21}}{3}$.
點評 此題主要考查了勾股定理以及全等三角形的判定與性質等知識,熟練應用全等三角形的判定方法是解題關鍵.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:初中數學 來源: 題型:選擇題
| A. | 設這個角是45° | B. | 設這個角是30° | C. | 設這個角是20° | D. | 設這個角是15° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
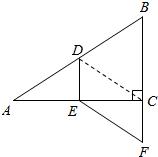 如圖,在Rt△ABC中,∠ACB=90°,點D,E分別是邊AB,AC的中點,延長BC至F,使CF=$\frac{1}{2}$BC,若AB=10,則EF的長是( )
如圖,在Rt△ABC中,∠ACB=90°,點D,E分別是邊AB,AC的中點,延長BC至F,使CF=$\frac{1}{2}$BC,若AB=10,則EF的長是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 環數 | 6 | 7 | 8 | 9 |
| 人數 | 1 | 5 | 3 | 1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com