
 如圖,點P在∠AOB的平分線上,若使△AOP≌△BOP,則需添加的一個條件是 .
如圖,點P在∠AOB的平分線上,若使△AOP≌△BOP,則需添加的一個條件是 .分析 (1)根據全等三角形的判定進行解答即可;
(2)添加∠APO=∠BPO,利用ASA判斷得出△AOP≌△BOP.
解答 解:(1)不認同,按小明添加的條件,就是用“邊邊角”證明全等;
(2)∠APO=∠BPO.
理由:∵點P在∠AOB的平分線上,
∴∠AOP=∠BOP,
在△AOP和△BOP中
$\left\{\begin{array}{l}{∠AOP=∠BOP}\\{OP=OP}\\{∠OPA=∠OPB}\end{array}\right.$,
∴△AOP≌△BOP(ASA),
故答案為:∠APO=∠BPO.
點評 此題主要考查了全等三角形的判定,全等三角形的5種判定方法中,選用哪一種方法,取決于題目中的已知條件,若已知兩邊對應相等,則找它們的夾角或第三邊;若已知兩角對應相等,則必須再找一組對邊對應相等,且要是兩角的夾邊,若已知一邊一角,則找另一組角,或找這個角的另一組對應鄰邊.


科目:初中數學 來源: 題型:選擇題
| A. | 6.8×10-7m | B. | 68×10-9m | C. | 0.68×10-7m | D. | 6.8×10-8m |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 已知雙曲線$y=\frac{k}{x}$(k<0,x>0)的圖象經過Rt△OAB斜邊OB的中點D,與直角邊AB相交于點C.若△OBC的面積為3,則k=-2.
已知雙曲線$y=\frac{k}{x}$(k<0,x>0)的圖象經過Rt△OAB斜邊OB的中點D,與直角邊AB相交于點C.若△OBC的面積為3,則k=-2.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 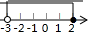 | B. |  | C. |  | D. | 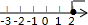 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,點D是AC邊上一點,以AD為直徑的⊙O與邊BC切于點E,且AB=BE.
如圖,在△ABC中,點D是AC邊上一點,以AD為直徑的⊙O與邊BC切于點E,且AB=BE.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com