
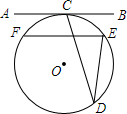
 如圖,直線AB與⊙O相切于點C,D是⊙O上的一點,∠CDE=22.5°,若EF∥AB,且EF=2,則⊙O的半徑是$\sqrt{2}$.
如圖,直線AB與⊙O相切于點C,D是⊙O上的一點,∠CDE=22.5°,若EF∥AB,且EF=2,則⊙O的半徑是$\sqrt{2}$. 分析 連接OE,OF,OC,根據圓周角定理得到∠COE=45°,根據切線的性質得到OC⊥AB根據平行線的性質得到OC⊥EF,求得∠FOE=2∠COE=90°,根據等腰直角三角形的性質即可得到結論.
解答 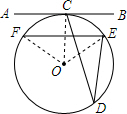 解:連接OE,OF,OC,
解:連接OE,OF,OC,
∵∠CDE=22.5°,
∴∠COE=45°,
∵直線AB與⊙O相切于點C,
∴OC⊥AB,
∵EF∥AB,
∴OC⊥EF,
∴∠FOE=2∠COE=90°,
∴OE=OF=$\frac{\sqrt{2}}{2}$EF=$\sqrt{2}$,
故答案為:$\sqrt{2}$.
點評 本題考查了切線的性質,圓周角定理,垂徑定理,等腰直角三角形的性質,正確的周長輔助線是解題的關鍵.


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:初中數學 來源: 題型:選擇題
 菱形ABCD的對角線AC、BD的長分別為4和2,若直線l滿足:①點A到直線l的距離為$\sqrt{3}$;②B、D兩點到直線l的距離相等.則符合題意的直線l的條數為( )
菱形ABCD的對角線AC、BD的長分別為4和2,若直線l滿足:①點A到直線l的距離為$\sqrt{3}$;②B、D兩點到直線l的距離相等.則符合題意的直線l的條數為( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點P在∠AOB的平分線上,若使△AOP≌△BOP,則需添加的一個條件是 .
如圖,點P在∠AOB的平分線上,若使△AOP≌△BOP,則需添加的一個條件是 .查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 近似數2.12萬精確到十分位 | |
| B. | 經過兩點有且只有一條直線 | |
| C. | 若ax=bx,則a=b | |
| D. | 若多項式5x|m|y2-(m-2)xy是四次二項式,則m=±2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 兩點之間,射線最短 | B. | 兩點確定一條直線 | ||
| C. | 兩點之間,直線最短 | D. | 兩點之間,線段最短 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com