
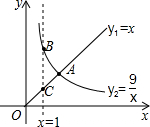
 函數y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的圖象如圖所示,則結論:
函數y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的圖象如圖所示,則結論:| A. | ①③④ | B. | ①②③④ | C. | ②③④ | D. | ①③ |
分析 ①聯立兩函數解析式,解方程組,再根據交點A在第一象限即可確定;
②根據函數圖象在上方的函數值大于在下方的函數值解答;
③利用兩個函數的解析式分別求出x=1時的函數值,相減即可得到BC的長度;
④分別根據一次函數的增減性與反比例函數的增減性進行判斷.
解答 解:①根據題意列解方程組$\left\{\begin{array}{l}{y=x}\\{y=\frac{9}{x}}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{{x}_{1}=3}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=-3}\end{array}\right.$;
∴這兩個函數在第一象限內的交點A的坐標為(3,3),故①正確;
②根據圖象可知,當x<3時,y1在y2的下方,故y1<y2,即y2>y1,故②正確;
③當x=1時,y1=1,y2=$\frac{9}{1}$=9,即點C的坐標為(1,1),點B的坐標為(1,9),所以BC=9-1=8,故③正確;
④由于y1=x(x≥0)的圖象自左向右呈上升趨勢,故y1隨x的增大而增大,
y2=$\frac{9}{x}$(x>0)的圖象自左向右呈下降趨勢,故y2隨x的增大而減小,故④正確.
故選B.
點評 本題考查了一次函數與反比例函數的交點問題,已知自變量求函數值,聯立兩函數解析式求交點,數形結合利用圖象求不等式的解,一次函數與反比例函數的增減性,難度適中.


科目:初中數學 來源: 題型:解答題
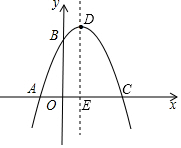 已知拋物線C1經過A(-1,0),B(0,3),C(3,0)三點,其頂點為點D,對稱軸與x軸交于點E.
已知拋物線C1經過A(-1,0),B(0,3),C(3,0)三點,其頂點為點D,對稱軸與x軸交于點E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com