
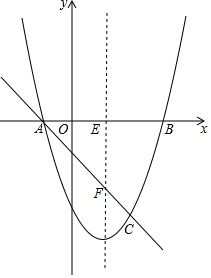
 如圖,拋物線y=x2-2x-3與x軸交于A、B兩點(diǎn)(A點(diǎn)在B點(diǎn)左側(cè)),點(diǎn)C為拋物線上一點(diǎn),且點(diǎn)C的橫坐標(biāo)為2,拋物線的對稱軸EF交x軸于點(diǎn)E,交直線AC于點(diǎn)F.
如圖,拋物線y=x2-2x-3與x軸交于A、B兩點(diǎn)(A點(diǎn)在B點(diǎn)左側(cè)),點(diǎn)C為拋物線上一點(diǎn),且點(diǎn)C的橫坐標(biāo)為2,拋物線的對稱軸EF交x軸于點(diǎn)E,交直線AC于點(diǎn)F.分析 (1)把y=0代入拋物線y=x2-2x-3可求得點(diǎn)A、B 的坐標(biāo),把x=2代入拋物線中可求得點(diǎn)C的坐標(biāo),利用待定系數(shù)法求直線AC的解析式;
(2)根據(jù)直徑所對的圓周角是直角畫出∠AGC=90°,確定點(diǎn)G的位置,有兩個(gè)符合條件的G點(diǎn),作輔助線,構(gòu)建直角三角形,先根據(jù)坐標(biāo)特點(diǎn)及中點(diǎn)定義得出D的坐標(biāo),計(jì)算AC的長,則半徑為$\frac{3\sqrt{2}}{2}$,根據(jù)勾股定理計(jì)算G1H的長,利用坐標(biāo)證明△AOM和△DMH是等腰直角三角形,從而得出點(diǎn)G的坐標(biāo);
(3)存在兩個(gè)P點(diǎn),根據(jù)切線長定理可知,①∠OMC的平分線與EF的交點(diǎn)為P,②∠GMC的平分線與EF的交點(diǎn)為P;作輔助線,構(gòu)建直角三角形,根據(jù)拋物線的對稱軸為x=1可知,P的橫坐標(biāo)為1,分別根據(jù)勾股定理和等腰直角三角形的性質(zhì)求縱坐標(biāo)即可.
解答 解:(1)當(dāng)y=0時(shí),x2-2x-3=0,
(x-3)(x+1)=0,
x1=3,x2=-1,
∵A點(diǎn)在B點(diǎn)左側(cè),
∴A(-1,0),B(3,0),
當(dāng)x=2時(shí),y=x2-2x-3=-3,
∴C(2,-3),
設(shè)直線AC的解析式為:y=kx+b,
把A(-1,0),C(2,-3)代入得:$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
∴直線AC的解析式為:y=-x-1;
(2)取AC的中點(diǎn)D,以D為圓心,以AD為半徑作圓交y軸于G1、G2,
連接DG1,DG2,過D作DH⊥y軸于H,
此時(shí)∠AG1C=∠AG2C=90°,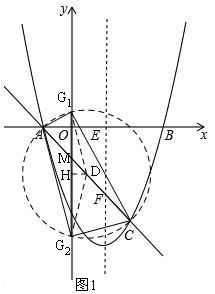
∵A(-1,0),C(2,-3),
∴D($\frac{1}{2}$,-$\frac{3}{2}$),AC=$\sqrt{(2+1)^{2}+(0+3)^{2}}$=3$\sqrt{2}$,
∴AD=DG1=$\frac{3}{2}\sqrt{2}$,
∵DH=$\frac{1}{2}$,
由勾股定理得:G1H=$\sqrt{(\frac{3\sqrt{2}}{2})^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{19}}{2}$,
設(shè)直線AC交y軸于M,
當(dāng)x=0時(shí),y=-1,
∴OM=1,
∵OA=1,
∴OA=OM,
∴△AOM是等腰直角三角形,
∴∠AMO=∠DMH=45°,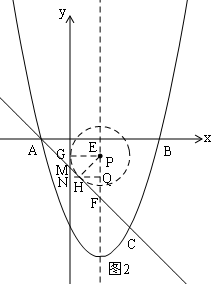
∴△DMH是等腰直角三角形,
∴DH=HM=$\frac{1}{2}$,
∴OG1=G1H-OH=$\frac{\sqrt{19}}{2}$-1-$\frac{1}{2}$=$\frac{\sqrt{19}-3}{2}$,
OG2=$\frac{\sqrt{19}}{2}$+1+$\frac{1}{2}$=$\frac{\sqrt{19}+3}{2}$,
∴點(diǎn)G的坐標(biāo)是(0,$\frac{\sqrt{19}-3}{2}$)或(0,-$\frac{\sqrt{19}+3}{2}$);
(3)存在,
如圖2,⊙P與y軸、AC都相切,切點(diǎn)分別為G、H,連接PG、PH,則PG⊥y軸,PH⊥AC,過H作NQ⊥y軸,則NQ⊥EF
∴△NMH是等腰直角三角形,
∵∠MHP=90°,
∴∠PHQ=45°,
∴△PHQ是等腰直角三角形,
∵PG=PH=1,
∴PQ=HQ=$\frac{\sqrt{2}}{2}$,
∴HN=NM=1-$\frac{\sqrt{2}}{2}$,
∵GN=PQ=$\frac{\sqrt{2}}{2}$,
∴GM=$\frac{\sqrt{2}}{2}$-(1-$\frac{\sqrt{2}}{2}$)=$\sqrt{2}$-1,
∴OG=1-($\sqrt{2}$-1)=2-$\sqrt{2}$,
∴P(1,$\sqrt{2}$-2);
如圖3,切點(diǎn)為G、H,連接PG、PH,則PG⊥y軸,PH⊥AC,
過H作NQ∥y軸,交GP的延長線于N,過M作MQ⊥y軸,則四邊形MGNQ是矩形,
∵PG=PH=1,∠GMH=45°,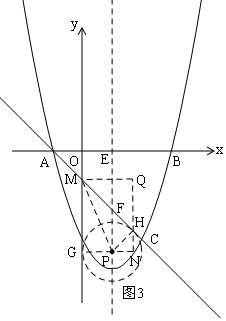
連接PM,則PM平分∠GMH,
∴∠GMP=∠PMH=22.5°,
∴∠HMQ=45°,
∴△MQH是等腰直角三角形,
∵∠GPM=∠MPH=67.5°,
∴∠NPH=45°,
∴△PNH是等腰直角三角形,
∴PN=NC=$\frac{\sqrt{2}}{2}$,
∴MQ=1+$\frac{\sqrt{2}}{2}$,
∴MG=QN=1+$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{2}$=$\sqrt{2}$+1,
∴OG=OM+MG=1+$\sqrt{2}$+1=2+$\sqrt{2}$,
∴P(1,-2-$\sqrt{2}$),
綜上所述,圓心P的坐標(biāo)是(1,$\sqrt{2}$-2)或(1,-2-$\sqrt{2}$).
點(diǎn)評 本題是二次函數(shù)與圓的綜合題,考查了利用待定系數(shù)法求一次函數(shù)的解析式、拋物線與x軸的交點(diǎn)、圓周角定理、切線長定理等知識,有難度,注意2、3問要分類討論,不要丟解,熟練掌握:①直徑所對的圓周角是直角;②從圓外一點(diǎn)引圓的切線,切線長相等,它與圓心的連線平分切線所在的夾角;本題的關(guān)鍵是確定點(diǎn)G和P的位置.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | y=2x+1 | B. | y=2x-1 | C. | y=2x+2 | D. | y=2x-2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 29,28 | B. | 30,29 | C. | 28,27 | D. | 29,29 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | AB=4,BC=5 | B. | AB=4,BC=3,∠A=30° | ||
| C. | ∠C=60°,AB=4 | D. | ∠A=90°,BC=5,AB=4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | (-3,-2) | B. | (2,-3) | C. | (2,3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com