
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
分析 欲判斷是否為勾股數,必須根據勾股數是正整數,同時還需驗證兩小邊的平方和是否等于最長邊的平方.
解答 解:①由于0.32+0.42=0.52,所以以0.3,0.4,0.5為邊長的三角形是直角三角形,但是0.3,0.4,0.5不是整數,所以0.3,0.4,0.5不是勾股數,故①說法錯誤;
②雖然以0.5,1.2,1.3為邊長的三角形是直角三角形,但是0.5,1.2,1.3不是整數,所以0.5,1.2,1.3不是勾股數,故②說法錯誤;
③若a,b,c是勾股數,且c最大,則一定有a2+b2=c2,故③說法正確;
④若三個整數a,b,c是直角三角形的三邊長,則2a,2b,2c一定是勾股數,故④說法正確.
故選C.
點評 此題考查了勾股數:滿足a2+b2=c2的三個正整數,稱為勾股數.注意:
①三個數必須是正整數,例如:2.5、6、6.5滿足a2+b2=c2,但是它們不是正整數,所以它們不是勾股數.
②一組勾股數擴大相同的整數倍得到的三個數仍是一組勾股數.
③記住常用的勾股數再做題可以提高速度.如:3,4,5;6,8,10;5,12,13;….


 名題金卷系列答案
名題金卷系列答案 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:解答題
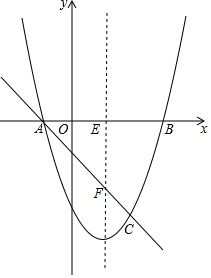 如圖,拋物線y=x2-2x-3與x軸交于A、B兩點(A點在B點左側),點C為拋物線上一點,且點C的橫坐標為2,拋物線的對稱軸EF交x軸于點E,交直線AC于點F.
如圖,拋物線y=x2-2x-3與x軸交于A、B兩點(A點在B點左側),點C為拋物線上一點,且點C的橫坐標為2,拋物線的對稱軸EF交x軸于點E,交直線AC于點F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
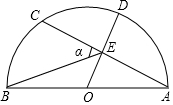 如圖,AB是半圓的直徑,點O為圓心,OA=5,弦AC=8,OD⊥AC,垂足為E,交⊙O于D,連接BE,設∠BEC=α,則tanα的值為( )
如圖,AB是半圓的直徑,點O為圓心,OA=5,弦AC=8,OD⊥AC,垂足為E,交⊙O于D,連接BE,設∠BEC=α,則tanα的值為( )| A. | $\frac{3}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,MQ為∠NMP的平分線,MP⊥NP,QT⊥MN,垂足分別為P,T,下列結論不正確的是( )
如圖,MQ為∠NMP的平分線,MP⊥NP,QT⊥MN,垂足分別為P,T,下列結論不正確的是( )| A. | S△MNQ=$\frac{1}{2}$MN•PQ | B. | ∠MQT=∠MQP | C. | MT=MP | D. | ∠NQP=∠MQT |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,⊙O是△ABC的內切圓,D,E是切點,∠A=50°,∠C=60°,則∠DOE的度數為( )
如圖,⊙O是△ABC的內切圓,D,E是切點,∠A=50°,∠C=60°,則∠DOE的度數為( )| A. | 70° | B. | 110° | C. | 120° | D. | 130° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -$\frac{1}{2}$<-2<0.02<0 | B. | -$\frac{1}{2}$<-2<0<0.02 | C. | -2<-$\frac{1}{2}$<0.02<0 | D. | -2<-$\frac{1}{2}$<0<0.02 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,點D,E分別在AB,AC上,則添加下面的條件后,不能判斷△AED∽△ABC的是( )
如圖,在△ABC中,點D,E分別在AB,AC上,則添加下面的條件后,不能判斷△AED∽△ABC的是( )| A. | $\frac{AD}{AC}$=$\frac{DE}{BC}$ | B. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | C. | ∠AED=∠B | D. | ∠ADE=∠C |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4 | B. | 2x-2 | C. | -4 | D. | 2-2x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com