
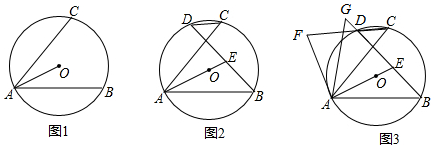
分析 (1)根據(jù)SSS證明△AOC≌△AOB,可得∠OAC=∠OAB;
(2)作輔助線,根據(jù)角平分線的性質(zhì)得PE=EH,證明Rt△APE≌Rt△AHE,得AP=AH,所以PC=BH,再證明△DPC≌△EHB,可得結(jié)論;
(3)如圖3,作輔助線,構(gòu)建△ACF的高線AH,設(shè)∠GAE=α,根據(jù)已知等式得α+20°=45°+$\frac{1}{2}α$,求出α=50°,得∠GAC=30°,根據(jù)三角函數(shù)表示AP=$\frac{\sqrt{3}}{2}$AG,代入△ACF面積公式進行計算即可.
解答  證明:(1)如圖1,連接OC、OB
證明:(1)如圖1,連接OC、OB
在△AOC和△AOB中,
∵$\left\{\begin{array}{l}{AC=AB}\\{AO=AO}\\{OC=OB}\end{array}\right.$
∴△AOC≌△AOB(SSS)
∴∠OAC=∠OAB;
(2)如圖2,過E作EH⊥AB于H,
∵BD⊥AC,∠OAC=∠OAB,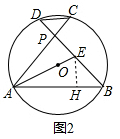
∴PE=EH,
∵AE=AE,
∴Rt△APE≌Rt△AHE(HL),
∴AP=AH,
∵AC=AB,
∴AC-AP=AB-AH,
即PC=BH,
∵∠C=∠B,∠DPC=∠EHB=90°,
∴△DPC≌△EHB,
∴BE=CD;
(3)如圖3,過A作AH⊥CF,設(shè)BG與AC交于點P,
∵∠B=50°,BD⊥AC,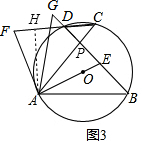
∴∠BAC=90°-50°=40°,
∵∠CAO=∠BAO,
∴∠CAO=∠BAO=20°,
設(shè)∠GAE=α,則α+20°=45°+$\frac{1}{2}α$,
α=50°,
∴∠GAC=30°,
在Rt△APG中,cos30°=$\frac{AP}{AG}$,
∴AP=$\frac{\sqrt{3}}{2}$AG,
∵AB=AC,∠B=∠C,∠AHC=∠APE=90°,
∴△ACH≌△ABP,
∴AH=AP=$\frac{\sqrt{3}}{2}$AG,
S△ACF=$\frac{1}{2}$AH•CF=$\frac{1}{2}×\frac{\sqrt{3}}{2}$AG•CF=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×8=2$\sqrt{3}$.
點評 本題是圓的綜合題,考查了三角形全等的性質(zhì)和判定、特殊角的三角函數(shù)、圓心角、弧、圓周角之間的關(guān)系等知識,第一問可以作直徑AD,利用同圓中弦相等,則所對的弧相等,半圓相等,再由等式的性質(zhì)得:$\widehat{CD}=\widehat{BD}$,則所對的圓周角相等得出結(jié)論;第三問有難度,得出AH=AP=$\frac{\sqrt{3}}{2}$AG是關(guān)鍵.


科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
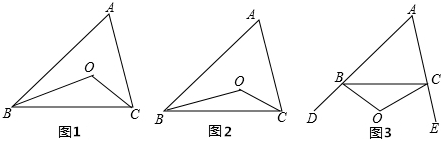
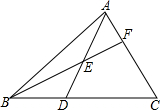 在△ABC中,D在BC上,E在AD上,連結(jié)BE,并延長交AC于F,若3BD=2CD,AE=DE,則$\frac{AF}{FC}$=$\frac{2}{5}$.
在△ABC中,D在BC上,E在AD上,連結(jié)BE,并延長交AC于F,若3BD=2CD,AE=DE,則$\frac{AF}{FC}$=$\frac{2}{5}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
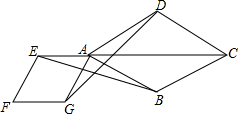 如圖,點E是菱形ABCD對角線CA的延長線上任意一點,以線段AE為邊作一個菱形AEFG,且∠EAG=∠BAD,連接EC,CD.
如圖,點E是菱形ABCD對角線CA的延長線上任意一點,以線段AE為邊作一個菱形AEFG,且∠EAG=∠BAD,連接EC,CD.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com