Question

（本題滿分10分）

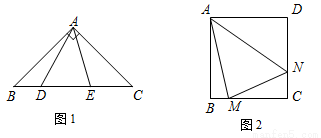
【操作探究】如圖1，在Rt△ABC中，∠BAC=90°，AB=AC，點D，E是BC邊上的任意兩點，且∠DAE=45°．

（1）將△ABD繞點A逆時針旋轉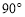，得到△ACF，請在圖（1）中畫出△ACF．

（2）在（1）中，連接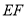，探究線段BD，EC和DE之間有怎樣的數量關系？寫出猜想，并說明理由．

【方法應用】

（3）如圖2，M，N分別是正方形ABCD的邊BC，CD上一點，且BM＋DN＝MN，試求∠MAN的大小．

 

 

Answer 1

（1）作圖見試題解析；（2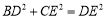），理由見試題解析；（3）45°．

【解析】

試題分析：（1）根據旋轉的性質，作出圖形即可；

（2）由旋轉的性質容易得到BD=CF，∠ECF=90°，再由△ADE≌△AFE，可得DE=EF，從而得到BD，EC和DE之間的數量關系；

（3）將△ABN繞點A逆時針旋轉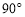，得到△ABE，從而得到E、B、M三點共線，在再由△AEM≌△ANM，即可得到∠MAN的度數．

試題解析：（1）如圖，

（2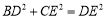），理由如下：

由旋轉可知，AF=AD，CF=BD，∠DAF=90°，

∵∠DAE=45°，∴∠DAE=∠FAE=45°，

在△DAE和△FAE中，∵AD=AF，∠CAE=∠EAF，AE=AE，∴△DAE≌△FAE（SAS），∴EF=DE，

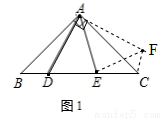
∵∠ECF=45°+45°=90°，∴，∴；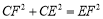

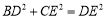（3） 將△ABN繞點A逆時針旋轉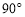，得到△ABE，如圖：

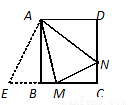
由旋轉得：∠NAE=90°，AN=AE，∠ABE=∠D=90°，∴E、B、M三點共線，

∵BM+DN=MN，∴ME=MN，

又∵AM=AM，∴△AEM≌△ANM，∴∠MAE=∠MAN=45°．

考點：1．旋轉的性質；2．全等三角形的判定與性質；3．正方形的性質．