
分析 (1)利用配方法,化成平方加一個正數(shù)的形式,可判斷其值為正數(shù);
(2)用a分別表示出S1與、S2,再作差比較即可.
解答 解:
(1)a2+6a+12=a2+6a+9+3=(a+3)2+3,
∵(a+3)2≥0,
∴(a+3)2+3≥3,
∴a2+6a+12的值一定是正數(shù);
(3)S1>S2,
理由:S1-S2=a2-4(a-3)=a2-4a+12=a2-4a+4+8=(a-2)2+8,
∵(a-2)2≥0,
∴(a-2)2+8≥8,
∴S1-S2>0,
∴S1>S2.
點評 本題主要考查配方法的應用,掌握配方法是解題的關鍵,注意兩數(shù)比較大小時可用作差法.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:解答題
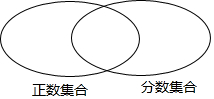 把下列各數(shù)填在相應的圓圈集合內(nèi):
把下列各數(shù)填在相應的圓圈集合內(nèi):查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
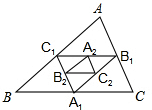 如圖,在△ABC中,A1、B1、C1分別是BC、CA、AB的中點,A2、B2、C2分別是B1C1、C1A1、A1B1的中點,…,An、Bn、Cn分別是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中點,假設△ABC的周長為a,則△A1B1C1的周長為$\frac{1}{2}$a,△A2B2C2的周長為$\frac{1}{4}$a,…,△AnBnCn的周長為$\frac{1}{{2}^{n}}$a.
如圖,在△ABC中,A1、B1、C1分別是BC、CA、AB的中點,A2、B2、C2分別是B1C1、C1A1、A1B1的中點,…,An、Bn、Cn分別是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中點,假設△ABC的周長為a,則△A1B1C1的周長為$\frac{1}{2}$a,△A2B2C2的周長為$\frac{1}{4}$a,…,△AnBnCn的周長為$\frac{1}{{2}^{n}}$a.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
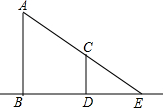 如圖,已知小魚同學的身高(CD)是1.6米,她與樹(AB)在同一時刻的影子長分別為DE=2米,BE=5米,那么樹的高度AB=4米.
如圖,已知小魚同學的身高(CD)是1.6米,她與樹(AB)在同一時刻的影子長分別為DE=2米,BE=5米,那么樹的高度AB=4米.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 正整數(shù)和正分數(shù)統(tǒng)稱正有理數(shù) | B. | 兩個無理數(shù)相乘的結果可能等于零 | ||
| C. | 正整數(shù),0,負整數(shù)統(tǒng)稱為整數(shù) | D. | 3.1415926是小數(shù),也是分數(shù) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 由5x=4x+1可得4x-5x=1 | B. | 由3(x-1)-2(2x-3)=1可得3x-3-4x-6=1 | ||
| C. | 由$\frac{x+2}{4}$-1=$\frac{2x-3}{6}$可得3(x+2)-1=2(2x-3) | D. | 由$\frac{1}{2}$x=$\frac{1}{4}$可得x=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
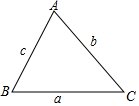 如圖,在銳角三角形中,
如圖,在銳角三角形中,查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com