Question

11．已知，點B為線段AC上的一個動點，△ACD與△BCE部為等邊三角形，點D與點E在直線AC的兩側，連接AE交DB的延長于點P．連接PC．
（1）如圖1，當點B為線段AC的中點時，求證：PA+PC=PD；
（2）如圖2，當點B不為線段AC的中點時，（1）的結論還成立嗎？若成立，請證明；若不成立，請說明理由．
（3）如圖3，分別過點C，E作CF⊥BD，EG⊥PC，垂足分別為點F，G，若PD-PA=5，BF=$\frac{5}{8}$，求線段CG的長．

Answer 1

分析 （1）根據等邊三角形的性質得到∠CDB=$\frac{1}{2}∠$ADC=30°，∠DBC=90°，證得PD垂直平分AC，根據線段垂直平分線的性質得到PA=PC，根據等邊三角形的性質得到AC=DC，∠ACE=∠DCB=60°，推出△ACE≌△DCB，根據全等三角形的性質得到∠CAE=∠CDB=30°，∠CEA=∠CBD=90°，即可得到結論；
（2）根據等邊三角形的性質得到AC=DC，∠ACE=∠DCB=60°，通過△ACE≌△DCB，得到∠CAE=∠CDB，∠CEA=∠CBD，以PC為邊作∠PCM=60°，另一邊交PD于M，證得△PCE≌△MCB，根據全等三角形的性質得到PC=CM，于是得到△PCM為等邊三角形，由等邊三角形的性質得到PC=PM=CM，求得∠DCM=∠ACP，根據全等三角形的性質得到PA=DM即可得到結論；
（3）由（2）知△PCM為等邊三角形，根據CF⊥BD，MF=PF和已知條件得到PD-DM=PM=5=PC=CM，于是得到MF=PF=$\frac{1}{2}$PM=$\frac{5}{2}$，根據全等三角形的性質得到BM=PE=$\frac{25}{8}$，∠EPC=∠PMC=60°，根據直角三角形的性質即可得到結論．

解答 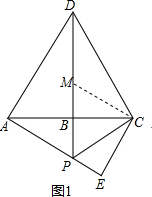證明：（1）∵△ACD為等邊三角形，點B為線段AC的中點，
∴∠CDB=$\frac{1}{2}∠$ADC=30°，∠DBC=90°，
∴PD垂直平分AC，
∴PA=PC，
∵△ACD與△BCE為等邊三角形，
∴AC=DC，∠ACE=∠DCB=60°，
在△ACE與△DCB中，
$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{EC=BC}\end{array}\right.$，
∴△ACE≌△DCB，
∴∠CAE=∠CDB=30°，∠CEA=∠CBD=90°，∠PAD=90°，
∴PD=2PA=2PC，
∴PD=PA+PC；

（2）∵△ACD與△BCE為等邊三角形，
∴AC=DC，∠ACE=∠DCB=60°，
在△ACE與△DCB中，
$\left\{\begin{array}{l}{AC=DC}\\{∠ACE=∠DCB}\\{EC=BC}\end{array}\right.$，
∴△ACE≌△DCB，
∴∠CAE=∠CDB，∠CEA=∠CBD，
以PC為邊作∠PCM=60°另一邊交PD于M，
∵∠PCM=∠BCE=60°，
∴∠MCB=∠PCE，
在△PCE與△MCB中，
$\left\{\begin{array}{l}{∠MCB=∠PCE}\\{BC=CE}\\{∠CEP=∠MBC}\end{array}\right.$，
∴△PCE≌△MCB，
∴PC=CM，
∴△PCM為等邊三角形，
∴PC=PM=CM，
∵∠PCM=∠ACD=60°，
∴∠DCM=∠ACP，
在△APC與△DMC中，
$\left\{\begin{array}{l}{AC=CD}\\{∠DCM=∠ACP}\\{PC=MC}\end{array}\right.$，
∴△APC≌△DMC，
∴PA=DM，
∴PA+PC=DM+PM=PD；

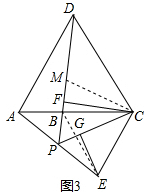
（3）解：由（2）知△PCM為等邊三角形，
∵CF⊥BD，MF=PF，
∵PD-PA=5，PA=DM，
∴PD-DM=PM=5=PC=CM，
∴MF=PF=$\frac{1}{2}$PM=$\frac{5}{2}$，
∵BF=$\frac{5}{8}$，
∴PB=$\frac{5}{2}$-$\frac{5}{8}$=$\frac{15}{8}$，
∵BM=PM-PB=5-$\frac{15}{8}$=$\frac{25}{8}$，
∵△PCE≌△MCB，
∴BM=PE=$\frac{25}{8}$，∠EPC=∠PMC=60°，
∵EG⊥PC，
∴∠PEG=30°，
∴$PG=\frac{1}{2}PE=\frac{25}{16}$，
∴CG=PC-PG=5-$\frac{25}{16}$=$\frac{55}{16}$．

點評 本題考查了全等三角形的判定和性質，等邊三角形的性質，線段垂直平分線的性質，正確的作出輔助線是解題的關鍵．