
分析 (1)設甲種獎品的單價為x元/個,乙種獎品的單價為y元/個,根據(jù)總價=單價×數(shù)量結合“購買甲獎品3個和乙獎品4個,需花64元;購買甲獎品4個和乙獎品5個,需花82元”即可得出關于x、y的二元一次方程組,解之即可得出結論;
(2)根據(jù)總價=單價×數(shù)量結合促銷方式即可得出y1、y2關于x的函數(shù)關系式;
(3)分0≤x≤6和x>6兩種情況考慮,當0≤x≤6時顯然購買甲種產品更省錢;當x>6時,分別令y1<y2、y1=y2、y1>y2,求出x的取值范圍.綜上即可得出結論.
解答 解:(1)設甲種獎品的單價為x元/個,乙種獎品的單價為y元/個,
根據(jù)題意得:$\left\{\begin{array}{l}{3x+4y=64}\\{4x+5y=82}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$.
答:甲種獎品的單價為8元/個,乙種獎品的單價為10元/個.
(2)根據(jù)題意得:y1=8×0.9x=7.2x;
當0≤x≤6時,y2=10x,
當x>6時,y2=10×6+10×0.6(x-6)=6x+24,
∴y2=$\left\{\begin{array}{l}{10x(0≤x≤6)}\\{6x+24(x>6)}\end{array}\right.$.
(3)當0≤x≤6時,
∵7.2<10,
∴此時買甲種產品省錢;
當x>6時,
令y1<y2,則7.2x<6x+24,
解得:x<20;
令y1=y2,則7.2x=6x+24,
解得:x=20;
令y1>y2,則7.2x>6x+24,
解得:x>20.
綜上所述:當x<20時,選擇甲種產品更省錢;當x=20時,選擇甲、乙兩種產品總價相同;當x>20時,選擇乙種產品更省錢.
點評 本題考查了二元一次方程組的應用、列代數(shù)式以及解一元一次不等式,解題的關鍵是:(1)根據(jù)數(shù)量關系列出關于x、y的二元一次方程組;(2)根據(jù)數(shù)量關系找出y1、y2關于x的函數(shù)關系式;(3)令y1<y2、y1=y2、y1>y2,求出x的取值范圍.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源: 題型:選擇題
| A. | 5個 | B. | 4個 | C. | 3個 | D. | 2個 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\frac{2}{3}$x=2 | B. | -$\frac{1}{4}$x+$\frac{1}{2}$=0 | C. | 3x+6=0 | D. | 5-3x=1 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
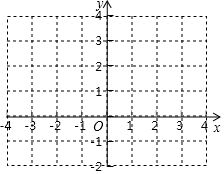 探索研究:通過對一次函數(shù)、反比例函數(shù)的學習.我們積累了一定的經驗.下面我們借鑒以往研究函數(shù)的經驗,探索y=$\frac{1}{|x|}$的圖象和性質.
探索研究:通過對一次函數(shù)、反比例函數(shù)的學習.我們積累了一定的經驗.下面我們借鑒以往研究函數(shù)的經驗,探索y=$\frac{1}{|x|}$的圖象和性質.| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 2 | 1 | $\frac{1}{2}$ | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com