
分析 把$\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$=2,兩邊同乘以$\sqrt{25-{x}^{2}}$+$\sqrt{15-{x}^{2}}$得到$\sqrt{15-{x}^{2}}$+$\sqrt{25-{x}^{2}}$=5,把40-2x2化為$\frac{1}{2}$($\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$)+($\sqrt{25-{x}^{2}}$+$\sqrt{15-{x}^{2}}$),代入即可得到結論.
解答 解:∵$\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$=2,
∴($\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$)($\sqrt{25-{x}^{2}}$+$\sqrt{15-{x}^{2}}$)=2($\sqrt{25-{x}^{2}}$+$\sqrt{15-{x}^{2}}$),
∴$\sqrt{15-{x}^{2}}$+$\sqrt{25-{x}^{2}}$=5,
∴40-2x2=25-x2+15-x2=$\frac{1}{2}$[($\sqrt{25-{x}^{2}}$-$\sqrt{15-{x}^{2}}$)2+($\sqrt{25-{x}^{2}}$+$\sqrt{15-{x}^{2}}$)2]
=$\frac{1}{2}$(22+52)=$\frac{29}{2}$.
點評 本題考查了二次根式的化簡求值,求得$\sqrt{15-{x}^{2}}$+$\sqrt{25-{x}^{2}}$=5是解題的關鍵.


 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:選擇題
 常數a,b,c在數軸上的位置如圖所示,則關于x的一元二次方程ax2+bx+c=0根的情況是( )
常數a,b,c在數軸上的位置如圖所示,則關于x的一元二次方程ax2+bx+c=0根的情況是( )| A. | 有兩個相等的實數根 | B. | 有兩個不相等的實數根 | ||
| C. | 無實數根 | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
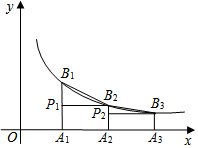 如圖,已知點A1、A2、A3、…、An在x軸上,且OA1=A1A2=A2A3═An-1An=1,分別過點A1、A2、A3、…、An作x軸的垂線,交反比例函數y=$\frac{2}{x}$(x>0)的圖象于點B1、B2、B3、…、Bn,過點B2作B2P1⊥A1B1于點P1,過點B3作B3P2⊥A2B2于點P2,…,若記△B1P1B2的面積為S1,△B2P2B3的面積為S2,…,△BnPnBn+1的面積為Sn,則S1+S2+…+S2017=$\frac{2017}{2018}$.
如圖,已知點A1、A2、A3、…、An在x軸上,且OA1=A1A2=A2A3═An-1An=1,分別過點A1、A2、A3、…、An作x軸的垂線,交反比例函數y=$\frac{2}{x}$(x>0)的圖象于點B1、B2、B3、…、Bn,過點B2作B2P1⊥A1B1于點P1,過點B3作B3P2⊥A2B2于點P2,…,若記△B1P1B2的面積為S1,△B2P2B3的面積為S2,…,△BnPnBn+1的面積為Sn,則S1+S2+…+S2017=$\frac{2017}{2018}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
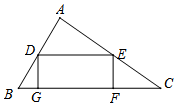 在△ABC中,BC=6,S△ABC=6,矩形DEFG內接于△ABC,其中點G、F在BC上,點D、E分別在AB、AC上,若DE:EF=k,求:四邊形DEFG的面積.
在△ABC中,BC=6,S△ABC=6,矩形DEFG內接于△ABC,其中點G、F在BC上,點D、E分別在AB、AC上,若DE:EF=k,求:四邊形DEFG的面積.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com