
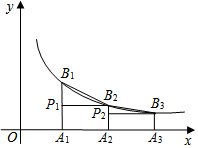
 如圖,已知點A1、A2、A3、…、An在x軸上,且OA1=A1A2=A2A3═An-1An=1,分別過點A1、A2、A3、…、An作x軸的垂線,交反比例函數y=$\frac{2}{x}$(x>0)的圖象于點B1、B2、B3、…、Bn,過點B2作B2P1⊥A1B1于點P1,過點B3作B3P2⊥A2B2于點P2,…,若記△B1P1B2的面積為S1,△B2P2B3的面積為S2,…,△BnPnBn+1的面積為Sn,則S1+S2+…+S2017=$\frac{2017}{2018}$.
如圖,已知點A1、A2、A3、…、An在x軸上,且OA1=A1A2=A2A3═An-1An=1,分別過點A1、A2、A3、…、An作x軸的垂線,交反比例函數y=$\frac{2}{x}$(x>0)的圖象于點B1、B2、B3、…、Bn,過點B2作B2P1⊥A1B1于點P1,過點B3作B3P2⊥A2B2于點P2,…,若記△B1P1B2的面積為S1,△B2P2B3的面積為S2,…,△BnPnBn+1的面積為Sn,則S1+S2+…+S2017=$\frac{2017}{2018}$. 分析 根據反比例函數圖象上點的坐標特征即可得出點B1、B2、B3、…、Bn的坐標,從而可得出B1P1、B2P2、B3P3、…、BnPn的長度,根據三角形的面積公式即可得出Sn=$\frac{1}{2}$AnAn+1•BnPn=$\frac{1}{n(n+1)}$,將其代入S1+S2+…+S2017中即可得出結論.
解答 解:根據題意可知:點B1(1,2)、B2(2,1)、B3(3,$\frac{2}{3}$)、…、Bn(n,$\frac{2}{n}$),
∴B1P1=2-1=1,B2P2=1-$\frac{2}{3}$=$\frac{1}{3}$,B3P3=$\frac{2}{3}$-$\frac{1}{2}$=$\frac{1}{6}$,…,BnPn=$\frac{2}{n}$-$\frac{2}{n+1}$=$\frac{2}{n(n+1)}$,
∴Sn=$\frac{1}{2}$AnAn+1•BnPn=$\frac{1}{n(n+1)}$,
∴S1+S2+…+S2017=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2017}$-$\frac{1}{2018}$=1-$\frac{1}{2018}$=$\frac{2017}{2018}$.
故答案為:$\frac{2017}{2018}$.
點評 本題考查了反比例函數圖象上點的坐標特征以及三角形的面積,根據反比例函數圖象上點的坐標特征結合三角形的面積找出Sn=$\frac{1}{2}$AnAn+1•BnPn=$\frac{1}{n(n+1)}$是解題的關鍵.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:選擇題
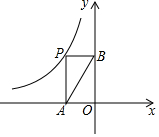 如圖,點P在反比例函數y=$\frac{k}{x}$的圖象上,PA⊥x軸于點A,PB⊥y軸于點B,且△APB的面積為2,則k等于( )
如圖,點P在反比例函數y=$\frac{k}{x}$的圖象上,PA⊥x軸于點A,PB⊥y軸于點B,且△APB的面積為2,則k等于( )| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 隨機拋擲一枚硬幣,反面一定朝上 | |
| B. | 數據3,3,5,5,8的眾數是8 | |
| C. | 某商場抽獎活動獲獎的概率為$\frac{1}{50}$,說明毎買50張獎券中一定有一張中獎 | |
| D. | 想要了解廣安市民對“全面二孩”政策的看法,宜采用抽樣調查 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 若m,n為正實數,t是關于x的方程x2+2mx=n2的一正實數根,
若m,n為正實數,t是關于x的方程x2+2mx=n2的一正實數根,查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com