

分析 (1)欲證明AD=CE,只要證明△ABD≌△CBE即可.
(2)如圖2中,倍長BE到H,連CH,DH.首先證明△DBH是等邊三角形,由(1)可知,△ABD≌△CBH,推出AD=CH,∠A=∠HCB=∠ABC=60°,推出BF∥CH,推出∠F=∠ECH,再證明△EBF≌△EHC,推出BF=CH,由此即可證明.
(3)如圖3中,作CH⊥AF于H.在Rt△CFH中,由∠F=45°,∠CHF=90°,推出∠F=∠HCF=45°,推出HF=HC=$\frac{\sqrt{2}}{2}$CF=3$\sqrt{2}$,在Rt△ACH中,由∠AHC=90°,∠A=60°,推出∠ACH=30°,推出AH=CH•tan30°=3$\sqrt{2}$×$\frac{\sqrt{3}}{3}$=$\sqrt{6}$,AF=3$\sqrt{2}$+$\sqrt{6}$,根據(jù)S△ACF=$\frac{1}{2}$•AF•CH計算即可.
解答 (1)證明:如圖1中,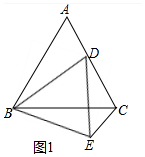
∵△ABC,△BDE都是等邊三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABD=∠CBE,
在△ABD和△CBE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠CBE}\\{BD=BE}\end{array}\right.$,
∴△ABD≌△CBE,
∴AD=CE.
(2)證明:如圖2中,倍長BE到H,連CH,DH.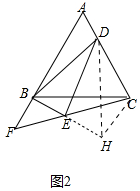
∵BE=EH,DE⊥BH,
∴DB=DH,∠BDE=∠HDE=30°,
∴∠BDH=60°,
∴△DBH是等邊三角形,
由(1)可知,△ABD≌△CBH,
∴AD=CH,∠A=∠HCB=∠ABC=60°,
∴BF∥CH,
∴∠F=∠ECH,
在△EBF和△EHC中,
$\left\{\begin{array}{l}{∠BEF=∠CEH}\\{∠F=∠ECH}\\{BE=EH}\end{array}\right.$,
∴△EBF≌△EHC,
∴BF=CH,
∴AD=CE.
(3)如圖3中,作CH⊥AF于H.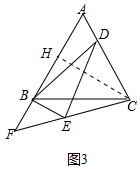
在Rt△CFH中,∵∠F=45°,∠CHF=90°,
∴∠F=∠HCF=45°,
∴HF=HC=$\frac{\sqrt{2}}{2}$CF=3$\sqrt{2}$,
在Rt△ACH中,∵∠AHC=90°,∠A=60°,
∴∠ACH=30°,
∴AH=CH•tan30°=3$\sqrt{2}$×$\frac{\sqrt{3}}{3}$=$\sqrt{6}$,
∴AF=3$\sqrt{2}$+$\sqrt{6}$,
∴S△ACF=$\frac{1}{2}$•AF•CH=$\frac{1}{2}$•(3$\sqrt{2}$+$\sqrt{6}$)•3$\sqrt{2}$=9+3$\sqrt{3}$.
點評 本題考查全等三角形的判定和性質(zhì)、等邊三角形的性質(zhì)、直角三角形30角度性質(zhì)、銳角三角函數(shù)等知識,解題的關(guān)鍵是學(xué)會添加輔助線構(gòu)造全等三角形,屬于中考壓軸題.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 已知y與x-3成正比例,當(dāng)x=4時,y=3.
已知y與x-3成正比例,當(dāng)x=4時,y=3.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
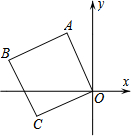 如圖,平面直角坐標(biāo)系中有一正方形OABC,點C的坐標(biāo)為(-4,-2).
如圖,平面直角坐標(biāo)系中有一正方形OABC,點C的坐標(biāo)為(-4,-2).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
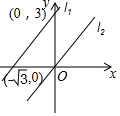 如圖,直線L1過點(0,3),(-$\sqrt{3}$,0).
如圖,直線L1過點(0,3),(-$\sqrt{3}$,0).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
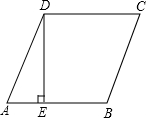 如圖所示,在菱形ABCD中,DE⊥AB于E,BE=16cm,sinA=$\frac{12}{13}$,求此菱形的周長.
如圖所示,在菱形ABCD中,DE⊥AB于E,BE=16cm,sinA=$\frac{12}{13}$,求此菱形的周長.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com