Question

13．如圖，直線l₁∥l₂，⊙O與l₁和l₂分別相切于點A和點B．直線MN與l₁相交于M，與l₂相交于N，⊙O的半徑為1，∠1=60°，直線MN從如圖所示位置向右平移，下列結(jié)論：①l₁和l₂的距離為2；②MN=4$\sqrt{3}$；③當直線MN與⊙O相切時，∠MON=90°；④當AM+BN=$\frac{{4\sqrt{3}}}{3}$時，直線MN與⊙O相切．其中正確的序號是①③④．

Answer 1

分析 如圖1，利用切線的性質(zhì)得到OA⊥l₁，OB⊥l₂，再證明點A、B、O共線即可得到l₁和l₂的距離為2，則可對①進行判斷；作NH⊥AM，如圖1，易得四邊形ABNH為矩形，則NH=AB=2，然后在Rt△MNH中利用含30度的直角三角形三邊的關(guān)系可計算出MN，從而可對②進行判斷；當直線MN與⊙O相切時，如圖2，利用切線長定理得到∠1=∠2，∠3=∠4，然后根據(jù)平行線的性質(zhì)和三角形內(nèi)角和可計算出∠MON的度數(shù)，則可對③進行判斷；過點O作OC⊥MN于C，如圖2，根據(jù)梯形的面積和三角形面積公式，利用S_{四邊形ABNM}=S_△OAM+S_△OMN+S_△OBN得到 $\frac{1}{2}$•1•AM+$\frac{1}{2}$•1•BN+$\frac{1}{2}$MN•OC=$\frac{1}{2}$（BN+AM）•2，則根據(jù)AM+BN=$\frac{4\sqrt{3}}{3}$，MN=$\frac{4\sqrt{3}}{3}$可計算出OC=1，然后根據(jù)切線的判定定理可判斷直線MN與⊙O相切，則可對④進行判斷．

解答 解：如圖1，∵⊙O與l₁和l₂分別相切于點A和點B，
∴OA⊥l₁，OB⊥l₂，
∵l₁∥l₂，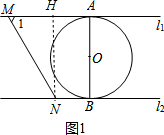
∴點A、B、O共線，
∴l(xiāng)₁和l₂的距離=AB=2，故①正確；
作NH⊥AM，如圖1，則四邊形ABNH為矩形，
∴NH=AB=2，
在Rt△MNH中，∵∠1=60°，
∴MH=$\frac{\sqrt{3}}{3}$NH=$\frac{2\sqrt{3}}{3}$，
∴MN=2MH=$\frac{4\sqrt{3}}{3}$，故②錯誤；
當直線MN與⊙O相切時，如圖2，∠1=∠2，∠3=∠4，
∵l₁∥l₂，
∴∠1+∠2+∠3+∠4=180°，
∴∠1+∠3=90°，
∴∠MON=90°，所以③正確；
過點O作OC⊥MN于C，如圖2，
∵S_{四邊形ABNM}=S_△OAM+S_△OMN+S_△OBN，
∴$\frac{1}{2}$•1•AM+$\frac{1}{2}$•1•BN+$\frac{1}{2}$•MN•OC=$\frac{1}{2}$•（BN+AM）•2，
即 $\frac{1}{2}$•（AM+BN）+MN•OC=AM+BN，
∵AM+BN=$\frac{4\sqrt{3}}{3}$，MN=$\frac{4\sqrt{3}}{3}$，
∴OC=1，
而OC⊥MN，
∴直線MN與⊙O相切，所以④正確．
故答案為①③④．

點評 本題考查了切線的判定與性質(zhì)：圓的切線垂直于經(jīng)過切點的半徑；經(jīng)過半徑的外端且垂直于這條半徑的直線是圓的切線．常見的輔助線的：判定切線時“連圓心和直線與圓的公共點”或“過圓心作這條直線的垂線”； 有切線時，常常“遇到切點連圓心得半徑”．