Question

8．如圖，已知矩形ABCD中，AB=4，AD=3，P是以CD為直徑的半圓上的一個動點，連接BP．
（1）半圓$\widehat{CD}$=2π； 
（2）BP的最大值是2+$\sqrt{13}$．

Answer 1

分析 （1）根據弧長公式進行計算即可；
（2）將以CD為直徑的⊙O補充完整，由點B在⊙O外可得出當點B、O、P三點共線時BP最大，根據矩形以及圓的性質可得出OC、OP的長度，再利用勾股定理即可求出OB的長度，進而即可得出BP的最大值．

解答 解：（1）$\widehat{CD}$=$\frac{180π•2}{180}$=2π；
（2）將以CD為直徑的⊙O補充完整，如圖所示．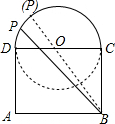
∵點B在⊙O外，
∴當點B、O、P三點共線時，BP的值最大．
∵CD為⊙O的直徑，CD=AB=4，
∴OC=OP=2．
在Rt△BOC中，BC=3，OC=2，
∴OB=$\sqrt{B{C}^{2}+O{C}^{2}}$=$\sqrt{13}$，
∴此時BP=BO+OP=$\sqrt{13}$+2．
故答案為：2π，$\sqrt{13}$+2．

點評 本題考查了點和圓的位置關系，矩形的性質以及弧長公式，掌握弧長公式和矩形的性質是解題的關鍵．