
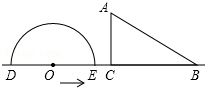
 如圖,半圓O直徑DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圓O從左到右運動,在運動過程中,點D,E始終在直線BC上,半圓O在△ABC的左側.
如圖,半圓O直徑DE=12,Rt△ABC中,BC=12,∠ACB=90°,∠ABC=30°.半圓O從左到右運動,在運動過程中,點D,E始終在直線BC上,半圓O在△ABC的左側.分析 (1)因為點D,E始終在直線BC,所以當△ABC的一邊與半圓O相切時只有三種情況,再分別畫出即可;
(2)本題要分當△ABC的一邊所在的直線與半圓O所在的圓相切時,半圓O與直徑DE圍成的區域與△ABC三邊圍成的區域有重疊部分的只有圖2與圖3所示的兩種情形分別計算即可.
解答 解:(1)如圖所示: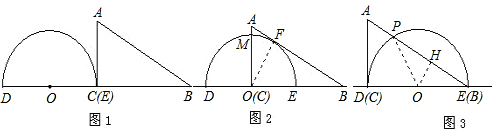
(2)當△ABC的一邊所在的直線與半圓O所在的圓相切時,半圓O與直徑DE圍成的區域與△ABC三邊圍成的區域有重疊部分的只有圖2與圖3所示的兩種情形.
①如圖2,設OA與半圓O的交點為M,易知重疊部分是圓心角為90°,半徑為6cm的扇形,所求重疊部分面積為:S扇形EOM=$\frac{1}{4}$π×62=9π(cm2)
②如圖3,設AB與半圓O的交點為P,連接OP,過點O作OH⊥AB,垂足為H.
則PH=BH.在Rt△OBH中,∠OBH=30°,OB=6cm
則OH=3cm,BH=3$\sqrt{3}$cm,BP=6$\sqrt{3}$cm,S△POB=$\frac{1}{2}$×6$\sqrt{3}$×3=9$\sqrt{3}$(cm2)
又因為∠DOP=2∠DBP=60°
所以S扇形DOP=6π(cm2)
所求重疊部分面積為:S△POB+S扇形DOP=9$\sqrt{3}$+6π(cm2),
綜上可知當半圓O與直徑DE圍成的區域與△ABC的三邊圍成的區域有重疊部分則重疊部分的面積是9π或9$\sqrt{3}$+6π.
點評 此題主要考查了切線的性質、扇形的面積公式,直角三角形的面積公式,銳角三角函數的概念、根據直線與圓的位置關系畫出符合題意的圖形是解題的關鍵.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案科目:初中數學 來源: 題型:填空題
 如圖,將一塊正方形空地劃出部分區域進行綠化,原空地一邊減少了2m,另一邊減少了3m,剩余一塊面積為20m2的矩形空地,若原正方形空地邊長是xm,則可列方程為(x-1)(x-3)=20.
如圖,將一塊正方形空地劃出部分區域進行綠化,原空地一邊減少了2m,另一邊減少了3m,剩余一塊面積為20m2的矩形空地,若原正方形空地邊長是xm,則可列方程為(x-1)(x-3)=20.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,P為正方形ABCD邊BC的中點,DE⊥AP于點E,F為AP上一點,AE=EF,∠CDF的平分線交AP的延長線于點G,連接CG,下列結論:①DE=2AE;②AG⊥CG;③△DEG為等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正確結論的個數是( )
如圖,P為正方形ABCD邊BC的中點,DE⊥AP于點E,F為AP上一點,AE=EF,∠CDF的平分線交AP的延長線于點G,連接CG,下列結論:①DE=2AE;②AG⊥CG;③△DEG為等腰直角三角形;④$\frac{CG}{AG}=\frac{1}{3}$.其中正確結論的個數是( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2和$\frac{1}{2}$ | B. | -0.5和$\frac{1}{2}$ | C. | -3和$\frac{1}{3}$ | D. | $\frac{1}{2}$和-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某校九年級數學興趣小組為了測得該校地下停車場的限高CD,在課外活動時間測得下列數據:如圖,從地面E點測得地下停車場的俯角為30°,斜坡AE的長為16米,地面B點(與E點在同一個水平線)距停車場頂部C點(A、C、B在同一條直線上且與水平線垂直)1.2米.試求該校地下停車場的高度AC及限高CD(結果精確到0.1米).
某校九年級數學興趣小組為了測得該校地下停車場的限高CD,在課外活動時間測得下列數據:如圖,從地面E點測得地下停車場的俯角為30°,斜坡AE的長為16米,地面B點(與E點在同一個水平線)距停車場頂部C點(A、C、B在同一條直線上且與水平線垂直)1.2米.試求該校地下停車場的高度AC及限高CD(結果精確到0.1米).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com