
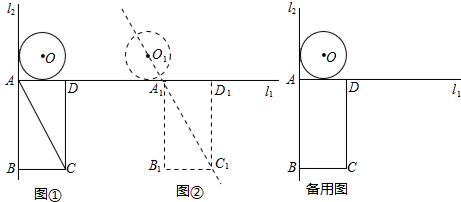
分析 (1)利用切線的性質以及銳角三角函數關系分別求出∠OAD=45°,∠DAC=60°,進而得出答案;
(2)首先求出∠C1A1D1=60°,再利用A1E=AA1-OO1-2=t-2,求出t的值,進而得出OO1=3t得出答案即可;
(3)由(2)得出∠C2A2D2=60°,∴∠GA2F=120°,求出∠O2A2F=60°,在Rt△A2O2F中,O2F=2,求出A2F=$\frac{2\sqrt{3}}{3}$,由OO2=3t1,AF=AA2+A2F=4t1+$\frac{2\sqrt{3}}{3}$,得出方程,解方程即可.
解答 解:(1)∵l1⊥l2,⊙O與l1,l2都相切,
∴∠OAD=45°,
∵四邊形ABCD是矩形,AC=8cm,
∴∠ABC=∠BAD=90°,BC=AD=4cm,CD=AB,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=4$\sqrt{3}$cm,
∴tan∠DAC=$\frac{CD}{AD}$=$\frac{4\sqrt{3}}{4}$=$\sqrt{3}$,
∴∠DAC=60°,
∴∠OAC=∠OAD+∠DAC=105°,
故答案為:105;故答案為:105;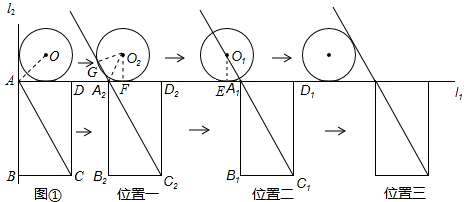 (2)如圖位置二,當O1,A1,C1恰好在同一直線上時,設⊙O1與l1的切點為E,
(2)如圖位置二,當O1,A1,C1恰好在同一直線上時,設⊙O1與l1的切點為E,
連接O1E,可得O1E=2,O1E⊥l1,
在Rt△A1D1C1中,∵A1D1=4,C1D1=4$\sqrt{3}$,
∴tan∠C1A1D1=$\sqrt{3}$,
∴∠C1A1D1=60°,
在Rt△A1O1E中,∠O1A1E=∠C1A1D1=60°,
∴A1E=$\frac{2}{tan60°}$=$\frac{2\sqrt{3}}{3}$,
∵A1E=AA1-OO1-2=t-2,
∴t-2=$\frac{2\sqrt{3}}{3}$,
∴t=$\frac{2\sqrt{3}}{3}$+2,
∴OO1=3t=2$\sqrt{3}$+6;即圓心O移動的距離為2$\sqrt{3}$+6;
(3)當直線AC與⊙O第一次相切時,移動時間為t1,
如圖位置一,此時⊙O移動到⊙O2的位置,矩形ABCD移動到A2B2C2D2的位置,
設⊙O2與直線l1,A2C2分別相切于點F,G,連接O2F,O2G,O2A2,
∴O2F⊥l1,O2G⊥A2C2,
由(2)得,∠C2A2D2=60°,
∴∠GA2F=120°,
∴∠O2A2F=60°,
在Rt△A2O2F中,O2F=2,
∴A2F=$\frac{2\sqrt{3}}{3}$,
∵OO2=3t1,AF=AA2+A2F=4t1+$\frac{2\sqrt{3}}{3}$,
∴4t1+$\frac{2\sqrt{3}}{3}$-3t1=2,
∴t1=2-$\frac{2\sqrt{3}}{3}$.
點評 本題是圓的綜合題目,考查了矩形的性質、切線的性質、勾股定理、直角三角形的性質、銳角三角函數等知識;本題綜合性強,有一定難度,熟練掌握矩形的性質和切線的性質是解決問題的關鍵.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $±\frac{1}{4}$ | D. | $±\frac{1}{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 兩點之間線段最短 | B. | 兩點確定一條直線 | ||
| C. | 垂線段最短 | D. | 過一點可以作無數條直線 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
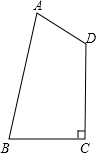 如圖,在四邊形ABCD中,AB=$\sqrt{5}$,AD=1,BC=CD=$\sqrt{2}$,且∠BCD=90°,試求四邊形ABCD的面積.
如圖,在四邊形ABCD中,AB=$\sqrt{5}$,AD=1,BC=CD=$\sqrt{2}$,且∠BCD=90°,試求四邊形ABCD的面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
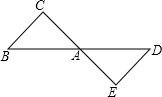 如圖,△ABC與△ADE關于點A成中心對稱.
如圖,△ABC與△ADE關于點A成中心對稱.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com