Question

方程x²-kx+k-2=0有兩個實數根x₁，x₂，且0＜x₁＜1，2＜x₂＜3，求k的取值范圍．

Answer 1

【答案】分析：由于方程x²-kx+k-2=0有兩個實數根x₁，x₂，且0＜x₁＜1，2＜x₂＜3，根據一元二次方程與二次函數的關系可畫出二次函數y=x²-kx+k-2的圖象，根據圖象得到當x=0，y=k-2＞0；當x=1，y=1-k+k-2＜0；當x=2，y=4-2k+k-2＜0；當x=3，y=9-3k+k-2＞0，求出幾個不等式解的公共部分即可得到k的取值范圍．
解答：解：∵方程x²-kx+k-2=0有兩個實數根x₁，x₂，且0＜x₁＜1，2＜x₂＜3，
∴二次函數y=x²-kx+k-2如圖所示，
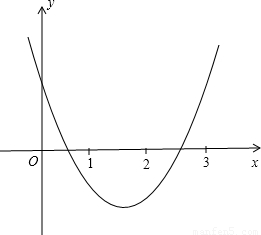
∴x=0，y=k-2＞0；x=1，y=1-k+k-2＜0；x=2，y=4-2k+k-2＜0；x=3，y=9-3k+k-2＞0，
而△=k²-4（k-2）=（k-2）²+4＞0，
∴2＜k＜，
即k的取值范圍為2＜k＜．
點評：本題考查了一元二次方程ax²+bx+c=0（a≠0）的根的判別式△=b²-4ac：當△＞0，方程有兩個不相等的實數根；當△=0，方程有兩個相等的實數根；當△＜0，方程沒有實數根．也考查了一元二次方程與二次函數的關系．