91在线精品一区二区,亚洲精品视频在线免费,亚洲第一国产精品

精英家教網 > 初中數學 > 題目詳情

17．

如圖，若干個全等的正五邊形排成環狀，圖中所示的是前3個正五邊形，要完成這一圓環還需正五邊形的個數為（　　）

A．

B．

C．

D．

分析先根據多邊形的內角和公式（n-2）•180°求出正五邊形的每一個內角的度數，再延長五邊形的兩邊相交于一點，并根據四邊形的內角和求出這個角的度數，然后根據周角等于360°求出完成這一圓環需要的正五邊形的個數，然后減去3即可得解．

解答解：∵五邊形的內角和為（5-2）•180°=540°，
∴正五邊形的每一個內角為540°÷5=108°，
如圖，延長正五邊形的兩邊相交于點O，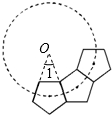
則∠1=360°-108°×3=360°-324°=36°，
360°÷36°=10，
∵已經有3個五邊形，
∴10-3=7，
即完成這一圓環還需7個五邊形．
故選D．

點評本題考查了多邊形的內角和公式，延長正五邊形的兩邊相交于一點，并求出這個角的度數是解題的關鍵，注意需要減去已有的3個正五邊形．

練習冊系列答案

必考點靈通復習法系列答案

名校調研系列卷每周一考系列答案

同步解析與測評初中總復習指導與訓練系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：解答題

7．小明在解決問題：已知a=$\frac{1}{2+\sqrt{3}}$，求2a²-8a+1的值，他是這樣分析與解答的：
∵a=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{（2+\sqrt{3}）（2-\sqrt{3}）}$=2-$\sqrt{3}$，
∴a-2=-$\sqrt{3}$，
∴（a-2）²=3，a²-4a+4=3
∴a²-4a=-1．
∴2a²-8a+1=2（a²-4a）+1=2（-1）+1=-1．
請你根據小明的分析過程，解決如下問題：若a=$\frac{1}{\sqrt{2}-1}$，求4a²-8a-3的值．

查看答案和解析>>

科目：初中數學 來源： 題型：填空題

8．

如圖，將周長為8cm的△ABC沿BC方向平移1cm得到△DEF，則四邊形ABFD的周長為10cm．

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

5．先化簡，再求值：（$\frac{1}{x-1}$-$\frac{1}{x+1}$）÷$\frac{2x+4}{{x}^{2}-1}$，其中x=-2+$\sqrt{2}$．

查看答案和解析>>

科目：初中數學 來源： 題型：選擇題

12．下列命題是真命題的是（　　）

	A．	非正數沒有平方根		B．	相等的角不一定是對頂角
	C．	同位角相等		D．	和為180°的兩個角一定是鄰補角

查看答案和解析>>

科目：初中數學 來源： 題型：解答題

2．

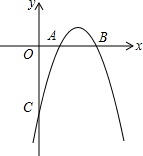如圖，拋物線y=ax²+bx+c與x軸交于點A（1，0），B（3，0），且過點C（0，-3）．
（1）則拋物線的解析式是y=-x²+4x-3頂點坐標是（2，1）；
（2）平移拋物線，使平移后拋物線的頂點落在直線y=-x上，且過原點O，求平移后拋物線的解析式；
（3）若原拋物線的頂點在射線y=0.5x（x＞0）上滑動，且過點（0，-14），應該怎樣平移原拋物線？

查看答案和解析>>

科目：初中數學 來源： 題型：填空題

9．若$\sqrt{x-1}$+$\sqrt{1-x}$=（x+y）²，則x-y=2．

查看答案和解析>>

科目：初中數學 來源： 題型：選擇題

6．如果$\sqrt{2}-1$是a的相反數，那么a的值是（　　）

A．

$1-\sqrt{2}$

B．

$1+\sqrt{2}$

C．

$-\sqrt{2}$