Question

18．綜合與實踐：制作禮品盒
如圖（1），小穎將邊長為60cm的正方形硬紙片ABCD，切去陰影部分所示的四個全等的等腰直角三角形，再沿虛線折起，如圖（2），點A，B，C，D四點重合于點P，做成一個底面是正方形的長方體形狀的禮品盒．設禮品盒的側面積為Scm²，AE=FB=xcm．

（1）求S與x之間的關系式及S的最大值；
（2）小穎有一底面半徑為15cm，高為15cm的圓柱體形狀的禮品，該禮品能否底面朝下放入她做成的禮品盒？若能，求出x的值；若不能，請說明理由．

Answer 1

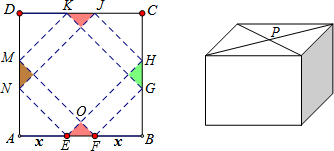
分析 （1）根據條件可以分別表示出陰影部分的面積，掀起的四個角上的四個等腰直角三角形的面積之和及底部正方形的面積就可以表示出S與x之間的函數關系式；將解析式化為頂點式就可以求出S的最大值；
（2）設包裝盒的底面正方形的邊長為a，高為h，就可以得出AE=$\frac{\sqrt{2}}{2}$a，EF=60-2AE=60-$\sqrt{2}$a，h=$\frac{\sqrt{2}}{2}$EF=30$\sqrt{2}$-a，再三種情況討論就可以得出結論．

解答 解：（1）∵AE=FB=xcm，
∴EF的長為（60-2x）cm．
圖中陰影部分拼在一起是邊長為EF的正方形，其面積為：（60-2x）²cm²，
掀起的四個角上的四個等腰直角三角形的面積之和為：2x²cm²；
盒底正方形的邊長為$\sqrt{2}$x，其面積為2x²；
∴S=60²-（60-2x）²-4x²=240x-8x²
∴S=-8（x²-30x）=-8（x-15）²+1800（0＜x＜30），
∵a=-8＜0．
∴拋物線的開口向下，S有最大值．
∴x=15cm時，側面積最大為1800cm²，
答：若包裝盒側面積S_最大=1800cm²最大，x應取15cm．

（2）包裝盒的底面正方形的邊長為a，高為h，
∴AE=$\frac{\sqrt{2}}{2}$a，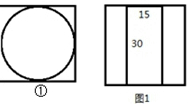
∴EF=60-2AE=60-$\sqrt{2}$a，
∴h=$\frac{\sqrt{2}}{2}$EF=30$\sqrt{2}$-a，
∴包裝盒的高h隨底面邊長的增大而減小．
圓柱的底面朝下放入，此時包裝盒高h不能小于15．
∵圓柱的底面半徑為15cm，
∴盒底邊長最小取30cm（放入如①圖），
∴h=30$\sqrt{2}$-a=30（$\sqrt{2}$-1）＜15，故不能放下．

點評 本題考查了勾股定理的運用，矩形的面積的運用，正方形的性質的運用，二次函數的解析式的運用，分類討論思想的運用，解答時分類討論是難點．