Question

13．如圖，在矩形ABCD中，AB=8，BC=12，點E為BC的中點．連接AE，將△ABE沿AE折疊，點B落在點F處，連接CF，現將△CEF繞點E順時針旋轉α角（其中0°≤α≤180°）得到△EC₁F₁，旋轉過程中，直線C₁F₁分別交射線EC、射線AE于點M、N，當EM=EN時，則CM=6-$\frac{12\sqrt{5}}{5}$．

Answer 1

分析 如圖作EK⊥FC，EJ⊥MN垂足分別為K、J，延長JE交AB于G，作GH⊥AE垂足為H，根據條件可以求出EK=EJ=$\frac{24}{5}$，BG=3，EG=3$\sqrt{5}$，利用△EBG∽△EJM求出EM，即可解決問題．

解答 解：如圖作EK⊥FC，EJ⊥MN垂足分別為K、J，延長JE交AB于G，作GH⊥AE垂足為H．
∵四邊形ABCD是矩形，AB=8，BC=12，BE=EC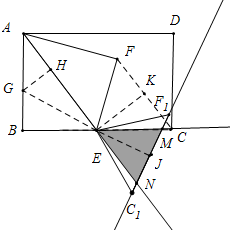
∴∠B=90°，BE=6，AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=10，
∵△AEF是△AEB翻折，
∴∠B=∠AFE=90°，∠BAE=∠EAF，
∴∠BAF+∠BEF=180°，
∵∠BEF+∠FEC=180°，
∴∠FEC=∠BAF，
∵EF=EC，EK⊥FC，
∴∠FEK=∠CEK，
∴∠BAE=∠CEK，
∵∠ABE=∠EKF，
∴△ABE∽△EKF，
∴$\frac{AE}{EF}=\frac{AB}{EK}$，即$\frac{10}{6}=\frac{8}{EK}$，
∴EK=$\frac{24}{5}$，
∵△EC₁F₁是由△EFC旋轉，EK⊥FC，EJ⊥F₁C₁，
∴EJ=EK=$\frac{24}{5}$，
∵EM=EN，EJ⊥MN，
∴∠MEJ=∠NEJ，
∵∠GEB=∠MEJ，∠GEH=∠NEJ，
∴∠GEB=∠GEH，∵GB⊥BE，GH⊥HE，
∴GB=GH，設GB=GH=x，
在RT△AGH中，由AG²=GH²+AH²，得（8-x）²=x²+4²，
∴x=3，
∴BG=GH=3，AG=5，
∴EG=$\sqrt{B{G}^{2}+B{E}^{2}}$=，3$\sqrt{5}$，
∵∠BEG=∠MEJ，∠B=∠EJM=90°，
∴△EBG∽△EJM，
∴$\frac{EG}{EM}=\frac{BE}{EJ}$，
∴$\frac{3\sqrt{5}}{EM}=\frac{6}{\frac{24}{5}}$，
∴EM=$\frac{12\sqrt{5}}{5}$，
∴CM=EC-EM=6-$\frac{12\sqrt{5}}{5}$．
故答案為6-$\frac{12\sqrt{5}}{5}$．

點評 本題考查了翻折和旋轉的有關性質、等腰三角形的性質、角平分線的性質、相似三角形的判定和性質、勾股定理等知識，構造三角形相似是解題關鍵．