
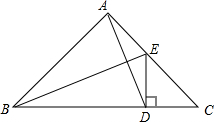
 如圖所示,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分線,DE⊥BC,垂足為D,且BC=15,求AB+AE的長.
如圖所示,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分線,DE⊥BC,垂足為D,且BC=15,求AB+AE的長. 分析 證明△ABE≌△DBE,則AE=DE,AB=BD,即可得到BE是線段AD的中垂線;根據AE=ED,以及△EDC是等腰直角三角形,即可得到AB+AE=BC,從而求解.
解答 解:在△ABE和△DBE中,
$\left\{\begin{array}{l}{∠BAE=∠BDE}\\{BE=BE}\\{∠ABE=∠DBE}\end{array}\right.$,
∴△ABE≌△DBE(ASA).
∴AE=DE,AB=BD,
∴B和E在AD的中垂線上.
∴AD⊥BE;
∵△ABC為等腰直角三角形,
∴∠C=45°,
∴直角△EDC是等腰直角三角形,
∴DE=AE.
∴AB+AE=BD+DE=BD+DC=BC=15(cm).
點評 本題考查了線段的垂直平分線的判定與性質,以及全等三角形的判定與性質,理解線段的垂直平分線的性質:線段的垂直平分線上的點到線段的兩端的距離相等,是關鍵.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x(x+3)=x2+3x | B. | 2n2-mn-n=2n(n-m-1) | ||
| C. | -x2-4y2+4xy=-(x-2y)2 | D. | 2x3-8x=2x(x2-4) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | “明天降雨的概率是75%”表示明天有75%的時間都在降雨 | |
| B. | “拋一枚硬幣正面朝上的概率為$\frac{1}{2}$”表示每拋2次就有1次正面朝上 | |
| C. | “拋一枚均勻的正方體骰子,朝上的點數是2的概率為$\frac{1}{6}$”表示隨著拋擲次數的增加,“拋出朝上的點數是2”這一事件發生的頻率穩定在$\frac{1}{6}$左右 | |
| D. | “彩票中獎的概率為1%”表示買100張彩票肯定會中獎 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
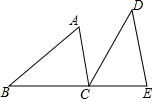 如圖,B、C、E三點在同一條直線上,AC∥DE,AC=CE,BC=DE.
如圖,B、C、E三點在同一條直線上,AC∥DE,AC=CE,BC=DE.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
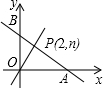 如圖,一次函數y=-x+m的圖象與x和y分別交于點A和點B,與正比例函數y=$\frac{3}{2}$x圖象交于點P(2,n).
如圖,一次函數y=-x+m的圖象與x和y分別交于點A和點B,與正比例函數y=$\frac{3}{2}$x圖象交于點P(2,n).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com