Question

14．已知∠AOB=100°，射線OC在∠AOB的內(nèi)部，射線OE，OF分別是∠AOC和∠COB的角平分線．

（1）如圖1，若∠AOC=30°，求∠EOF的度數(shù)；
（2）請從下面A，B兩題中任選一題作答，我選擇A題．
A．如圖2，若射線OC在∠AOB的內(nèi)部繞點(diǎn)O旋轉(zhuǎn)，則∠EOF的度數(shù)為50°．
B．若射線OC在∠AOB的外部繞點(diǎn)O旋轉(zhuǎn)（旋轉(zhuǎn)中∠AOC、∠BOC均是指小于180°的角），其余條件不變，請借助圖3探究∠EOF的大小，直接寫出∠EOF的度數(shù)．

Answer 1

分析 （1）先求出∠BOC度數(shù)，根據(jù)角平分線定義求出∠EOC和∠FOC度數(shù)，求和即可得出答案；
（2）A．根據(jù)角平分線定義得出∠COE=$\frac{1}{2}$∠AOC，∠COF=$\frac{1}{2}$∠BOC，求出∠EOF=∠EOC+∠FOC=$\frac{1}{2}$∠AOB，代入求出即可；
B．分兩種情況：①射線OE，OF只有1個在∠AOB外面，根據(jù)角平分線定義得出∠COE=$\frac{1}{2}$∠AOC，∠COF=$\frac{1}{2}$∠BOC，求出∠EOF=∠FOC-∠COE=$\frac{1}{2}$∠AOB；②射線OE，OF2個都在∠AOB外面，根據(jù)角平分線定義得出∠EOF=$\frac{1}{2}$∠AOC，∠COF=$\frac{1}{2}$∠BOC，求出∠EOF=∠EOC+∠COF=$\frac{1}{2}$（360°-∠AOB），代入求出即可．

解答 解：（1）∵∠AOB=100°，∠AOC=30°，
∴∠BOC=∠AOB-∠AOC=70°，
∵OE，OF分別是∠AOC和∠COB的角平分線，
∴∠EOC=$\frac{1}{2}$∠AOC=15°，∠FOC=$\frac{1}{2}$∠BOC=35°，
∴∠EOF=∠EOC+∠FOC=15°+35°=50°；

（2）A．∵OE，OF分別是∠AOC和∠COB的角平分線，
∴∠EOC=$\frac{1}{2}$∠AOC，∠FOC=$\frac{1}{2}$∠BOC，
∴∠EOF=∠EOC+∠FOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×100°=50°；

B．①射線OE，OF只有1個在∠AOB外面，如圖3①，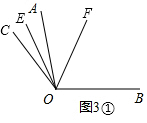

∠EOF=∠FOC-∠COE=$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC=$\frac{1}{2}$（∠BOC-∠AOC）=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×100°=50°．
②射線OE，OF2個都在∠AOB外面，如圖3②，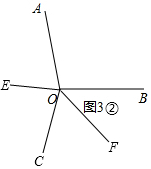

∠EOF=∠EOC+∠COF=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$（∠AOC+∠BOC）=$\frac{1}{2}$（360°-∠AOB）=$\frac{1}{2}$×260°=130°．
故∠EOF的度數(shù)是50°或130°．
故答案為：A，50°．

點(diǎn)評 本題考查的是角的計算，角平分線的定義，熟知從一個角的頂點(diǎn)出發(fā)，把這個角分成相等的兩個角的射線叫做這個角的平分線是解答此題的關(guān)鍵．注意分類思想的運(yùn)用．