
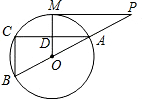
 如圖,MP切⊙O于點M,直線PO交⊙O于點A、B,弦AC∥MP,交OM于點D.
如圖,MP切⊙O于點M,直線PO交⊙O于點A、B,弦AC∥MP,交OM于點D.分析 (1)由切線的性質(zhì)可知OM⊥MP,結(jié)合條件可證得MO⊥AC,由圓周角定理可求得∠BCA=90°,則可證得BC∥OM;
(2)連接OC,設(shè)半徑為r,則可知OC=OM=r,由垂徑定理可求得CD,在Rt△COD中,利用勾股定理可列方程,可求得圓的半徑.
解答 (1)證明:
∵MP切⊙O于點M,
∴OM⊥MP,
∵AC∥MP,
∴OM⊥AC,
∴∠ODA=90°,
∵AB是直徑,
∴∠BCA=90°,
∴MO∥BC;
(2)解:
連結(jié)OC,設(shè)⊙O的半徑為r,則OC=OM=r.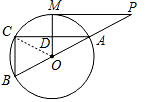
∵OM⊥AC,
∴CD=$\frac{1}{2}$AC=3,OD=OM-DM=r-2,
在Rt△OCD中,OC2=OD2+CD2,即r2=(r-2)2+32,
解得,r=$\frac{13}{4}$,即⊙O的半徑為$\frac{13}{4}$.
點評 本題主要考查切線的性質(zhì),掌握過切點的半徑與切線垂直是解題的關(guān)鍵.


 超能學(xué)典應(yīng)用題題卡系列答案
超能學(xué)典應(yīng)用題題卡系列答案科目:初中數(shù)學(xué) 來源: 題型:填空題
 如圖,在紙上剪下一個圓形和一個扇形的紙片,使之恰好能圍成一個圓錐模型.若圓的半徑為r,扇形的半徑為R,扇形的圓心角等于90°,則R與r之間的關(guān)系是R=4r.
如圖,在紙上剪下一個圓形和一個扇形的紙片,使之恰好能圍成一個圓錐模型.若圓的半徑為r,扇形的半徑為R,扇形的圓心角等于90°,則R與r之間的關(guān)系是R=4r.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
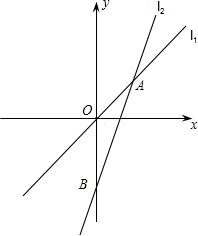 如圖,在平面直角坐標(biāo)系中,直線l1:y=$\frac{4}{3}$x與直線l2:y=kx+b相交于點A,點A的橫坐標(biāo)為3,直線l2交y軸于點B,且OA=$\frac{1}{2}$OB.
如圖,在平面直角坐標(biāo)系中,直線l1:y=$\frac{4}{3}$x與直線l2:y=kx+b相交于點A,點A的橫坐標(biāo)為3,直線l2交y軸于點B,且OA=$\frac{1}{2}$OB.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 對于平面直角坐標(biāo)系中的任意兩點P1(x1,y1),P2(x2,y2),我們把|x1-x2|+|y1-y2|叫做P1、P2兩點間的直角距離,記作d(P1,P2).
對于平面直角坐標(biāo)系中的任意兩點P1(x1,y1),P2(x2,y2),我們把|x1-x2|+|y1-y2|叫做P1、P2兩點間的直角距離,記作d(P1,P2).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,當(dāng)刻度尺的一邊與⊙O相切時,另一邊與⊙O的兩個交點處的讀數(shù)如圖所示(單位:cm),圓的半徑是5,那么刻度尺的寬度為( )
如圖,當(dāng)刻度尺的一邊與⊙O相切時,另一邊與⊙O的兩個交點處的讀數(shù)如圖所示(單位:cm),圓的半徑是5,那么刻度尺的寬度為( )| A. | $\frac{25}{6}$cm | B. | 4cm | C. | 3cm | D. | 2cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
| 第1個 | 第2個 | 第3個 | 第4個 | … |
| $\sqrt{{1^2}+1}$ | $\sqrt{{2^2}+2}$ | $\sqrt{{3^2}+3}$ | $\sqrt{{4^2}+4}$ | … |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 一個表面標(biāo)有漢字的多面體的平面展開圖如圖所示,如果“你”在上面,“樂”在前面,則不正確的是( )
一個表面標(biāo)有漢字的多面體的平面展開圖如圖所示,如果“你”在上面,“樂”在前面,則不正確的是( )| A. | “年”在下面 | B. | “祝”在后面 | C. | “新”在左邊 | D. | “快”在左邊 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com