
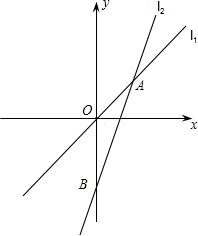
 如圖,在平面直角坐標系中,直線l1:y=$\frac{4}{3}$x與直線l2:y=kx+b相交于點A,點A的橫坐標為3,直線l2交y軸于點B,且OA=$\frac{1}{2}$OB.
如圖,在平面直角坐標系中,直線l1:y=$\frac{4}{3}$x與直線l2:y=kx+b相交于點A,點A的橫坐標為3,直線l2交y軸于點B,且OA=$\frac{1}{2}$OB.分析 (1)把點A的橫坐標代入進行解答即可;
(2)根據直線的平移特點進行解答即可.
解答 解:(1)根據題意,點A的橫坐標為3,代入直線l1:$y=\frac{4}{3}x$中,
得點A的縱坐標為4,即點A(3,4);
即OA=5,又|OA|=$\frac{1}{2}$|OB|.
即OB=10,且點B位于y軸上,
即得B(0,-10);
將A、B兩點坐標代入直線l2中,得4=3k+b;
-10=b;
解之得,k=$\frac{14}{3}$,b=-10;
即直線l2的解析式為y=$\frac{14}{3}$x-10;
(2)根據題意,平移后的直線l1的直線方程為$y=\frac{4}{3}(x+3)=\frac{4}{3}x+4$;
即點C的坐標為(0,4);
聯立線l2的直線方程,解得x=$\frac{21}{5}$,y=$\frac{28}{5}$,
即點D($\frac{21}{5}$,$\frac{28}{5}$);
又點B(0,-10),如圖所示:
故△BCD的面積S=$\frac{1}{2}×\frac{21}{5}×14=\frac{147}{5}$.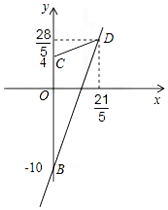
點評 此題考查一次函數與幾何變換問題,關鍵是根據直線的平移特點進行解答.


 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案 小題狂做系列答案
小題狂做系列答案科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,二次函數y=ax2+bx+6的圖象交x軸于A、B兩點,交y軸于點D,點C為拋物線的頂點,且A、B兩點的橫坐標分別為1和3.
如圖,在平面直角坐標系中,二次函數y=ax2+bx+6的圖象交x軸于A、B兩點,交y軸于點D,點C為拋物線的頂點,且A、B兩點的橫坐標分別為1和3.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于點D,則下列結論不正確的是( )
如圖,在Rt△ABC中,∠BAC=90°,AD⊥BC于點D,則下列結論不正確的是( )| A. | cosC=$\frac{CD}{AC}$ | B. | cosC=$\frac{AC}{BC}$ | C. | cosC=$\frac{AD}{AC}$ | D. | cosC=$\frac{AD}{AB}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
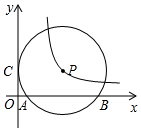 如圖,⊙P與y軸相切于點C(0,3),與x軸相交于點A(1,0),B(9,0).雙曲線y=$\frac{k}{x}$恰好經過圓心P,那么k的值是15.
如圖,⊙P與y軸相切于點C(0,3),與x軸相交于點A(1,0),B(9,0).雙曲線y=$\frac{k}{x}$恰好經過圓心P,那么k的值是15.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
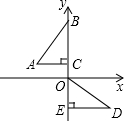 如圖,在平面直角坐標系中,點B、C、E在y軸上,Rt△ABC經過變換得到Rt△ODE,若點C的坐標為(0,1),AC=2,則這種變換可以是( )
如圖,在平面直角坐標系中,點B、C、E在y軸上,Rt△ABC經過變換得到Rt△ODE,若點C的坐標為(0,1),AC=2,則這種變換可以是( )| A. | △ABC繞點C逆時針旋轉90°,再向下平移1 | |
| B. | △ABC繞點C逆時針旋轉90°,再向下平移3 | |
| C. | △ABC繞點C順時針旋轉90°,再向下平移1 | |
| D. | △ABC繞點C順時針旋轉90°,再向下平移3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
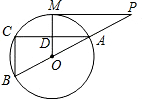 如圖,MP切⊙O于點M,直線PO交⊙O于點A、B,弦AC∥MP,交OM于點D.
如圖,MP切⊙O于點M,直線PO交⊙O于點A、B,弦AC∥MP,交OM于點D.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com