
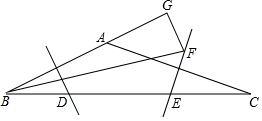
 如圖,在△ABC中,∠BAC為鈍角,邊AB、AC的垂直平分線分別交BC于點D、E.
如圖,在△ABC中,∠BAC為鈍角,邊AB、AC的垂直平分線分別交BC于點D、E.分析 (1)如圖1中,連接AD、AE.首先證明∠DAE=90°,易知∠DBA=∠DAB,∠EAC=∠C,設∠DBA=∠DAB=x,∠EAC=∠C=y,根據三角形內角和定理可得2x+90°+2y=180°,
推出x+y=45°,由此即可解決問題.
(2)如圖2中,連接AF,FC,作FM⊥CB于M,只要證明Rt△BFG≌Rt△CFM,Rt△AFG≌Rt△CFM,即可解決問題.
解答 解:(1)如圖1中,連接AD、AE.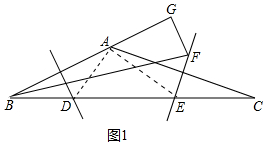
∵邊AB、AC的垂直平分線分別交BC于點D、E,
∴BD=DA,EA=EC,
∴∠DBA=∠DAB,∠EAC=∠C,設∠DBA=∠DAB=x,∠EAC=∠C=y,
∵BD2+CE2=DE2,
∴AD2+AE2=DE2,
∴∠DAE=90°,
∴2x+90°+2y=180°,
∴x+y=45°,
∴∠BAC=x+y+90°=135°.
(2)證明:如圖2中,連接AF,FC,作FM⊥CB于M,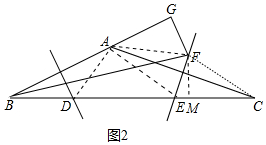
∵BF平分∠CBA,FG⊥BA,FM⊥CB,
∴FG=FM(角平分線上的點到角的兩邊距離相等),
在Rt△BFG和Rt△BFM中,
$\left\{\begin{array}{l}{BF=BF}\\{FG=FM}\end{array}\right.$
∴Rt△BFG≌Rt△CFM,
∴BG=BM,
∵EF垂直平分線AC,
∴FA=FC(垂直平分線上的點到線段兩端點距離相等),
∵FG=FM,∠AFD=∠DMB=90°,
在Rt△AFG和Rt△CFM中,
$\left\{\begin{array}{l}{FG=FM}\\{FA=FC}\end{array}\right.$,
∴Rt△AFG≌Rt△CFM,
∴CM=AG,
∵BC=BM+CM,BG=AB+AG,BG=BM,CM=AG,
∴BC=AB+2AG,
∴BC-AB=2AG.
點評 此題主要考查了全等三角形的判定和性質、線段的垂直平分線的性質、角平分線的性質、勾股定理的逆定理等知識,根據已知角平分線以及垂直平分線作出相關輔助線從而利用全等求出是解決問題的關鍵.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
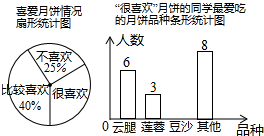 中秋佳節我國有賞月和吃月餅的傳統,某校數學興趣小組為了了解本校學生喜愛月餅的情況,隨機抽取了60名同學進行問卷調查,經過統計后繪制了兩幅尚不完整的統計圖.(注:參與問卷調查的每一位同學在任何一種分類統計中只有一種選擇)
中秋佳節我國有賞月和吃月餅的傳統,某校數學興趣小組為了了解本校學生喜愛月餅的情況,隨機抽取了60名同學進行問卷調查,經過統計后繪制了兩幅尚不完整的統計圖.(注:參與問卷調查的每一位同學在任何一種分類統計中只有一種選擇)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
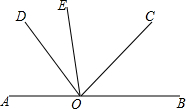 如圖,已知,A、O、B在同一條線上,∠AOE=∠COD,∠EOD=30°.
如圖,已知,A、O、B在同一條線上,∠AOE=∠COD,∠EOD=30°.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 若a>0,b>0,則a+b>0 | B. | 對頂角相等 | ||
| C. | 全等三角形的對應角相等 | D. | 平行四邊形的兩組對邊分別相等 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m=1,n=2 | B. | m=0,n=2 | C. | m=2,n=1 | D. | m=1,n=1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com