

分析 (1)如答圖1所示,過點A作AG⊥BC于點G,構造Rt△APG,利用勾股定理求出AP的長度;
(2)如答圖2所示,符合條件的點P有兩個.解直角三角形,利用特殊角的三角函數值求出角的度數;
(3)先判斷出AP∥FQ,進而得出AP⊥BC,即可求出AP=BP=CP=$\frac{3}{2}$,最后用四邊形的面積公式即可得出結論.
解答 解:(1)依題意畫出圖形,如答圖1所示: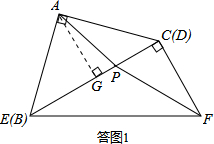
由題意,得∠CFB=60°,FP為角平分線,則∠CFP=30°,
∴CF=BC•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∴CP=CF•tan∠CFP=$\sqrt{3}×\frac{\sqrt{3}}{3}$=1.
過點A作AG⊥BC于點G,則AG=$\frac{1}{2}$BC=$\frac{3}{2}$,
∴PG=CG-CP=$\frac{3}{2}$-1=$\frac{1}{2}$.
在Rt△APG中,由勾股定理得:
AP=$\sqrt{A{G}^{2}+P{G}^{2}}$=$\frac{\sqrt{10}}{2}$.
(2)由(1)可知,FC=$\sqrt{3}$.
如答圖2所示,以點A為圓心,以FC=$\sqrt{3}$長為半徑畫弧,與BC交于點P1、P2,則AP1=AP2=$\sqrt{3}$.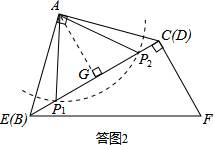
過點A過AG⊥BC于點G,則AG=$\frac{1}{2}$BC=$\frac{3}{2}$.
在Rt△AGP1中,cos∠P1AG=$\frac{AG}{A{P}_{1}}=\frac{\frac{3}{2}}{\sqrt{3}}$=$\frac{\sqrt{3}}{2}$;
∴∠P1AG=30°,
∴∠P1AB=45°-30°=15°;
同理求得,∠P2AG=30°,∠P2AB=45°+30°=75°.
∴∠PAB的度數為15°或75°.
(3)如答圖3,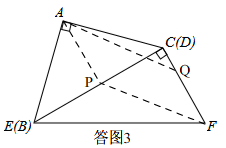
∵以A、P、F、Q為頂點的平行四邊形的頂點Q恰好在邊FC上,
∴AP∥QF,
∴∠APC=∠BCF,
∵∠BCF=90°,
∴∠APC=90°,
在R△ABC中,∠ABC=45°,BC=3,
∴AC=AB=$\frac{3\sqrt{2}}{2}$,
∴AP=BP=CP=$\frac{1}{2}$BC=$\frac{3}{2}$,
∴S平行四邊形APFQ=AP×PC=$\frac{3}{2}$×$\frac{3}{2}$=$\frac{9}{4}$,
即:點P運動到BC中點的位置時,以A、P、F、Q為頂點的平行四邊形的頂點Q恰好在邊FC上,且面積是$\frac{9}{4}$.
點評 此題是四邊形綜合題,主要考查了角平分線的意義,銳角三角函數,勾股定理,等腰直角三角形的性質,解本題的關鍵是特殊直角三角形的性質的運用.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
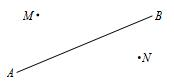 如圖,一輛汽車在筆直的公路AB上由A向B行駛,M、N分別是位于公路AB兩側的村莊,設行駛至點P時,離村莊M最近,汽車行駛到點Q時,離村莊N最近,汽車行駛到點O時,到村莊M、N的距離之和最小,請在圖中公路AB上分別畫出點P、Q、O的位置,并說明理由.
如圖,一輛汽車在筆直的公路AB上由A向B行駛,M、N分別是位于公路AB兩側的村莊,設行駛至點P時,離村莊M最近,汽車行駛到點Q時,離村莊N最近,汽車行駛到點O時,到村莊M、N的距離之和最小,請在圖中公路AB上分別畫出點P、Q、O的位置,并說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -8、-10 | B. | -8、10 | C. | 8、-10 | D. | 8、10 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{2-x}$ | B. | $\sqrt{x-2}$ | C. | -$\sqrt{2-x}$ | D. | -$\sqrt{x-2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖反映的過程是小明從家去食堂吃早餐,接著去圖書館讀報,然后回家,其中x表示時間,y表示小明離家的距離,小明家、食堂、圖書館在同一直線上,根據圖中提供的信息,下列說法正確的有( )
如圖反映的過程是小明從家去食堂吃早餐,接著去圖書館讀報,然后回家,其中x表示時間,y表示小明離家的距離,小明家、食堂、圖書館在同一直線上,根據圖中提供的信息,下列說法正確的有( )| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (-2$\sqrt{3}$)2=6 | B. | $\sqrt{1\frac{25}{49}}$=1$\frac{5}{7}$ | ||
| C. | $\sqrt{(-121)×(-9)}$=$\sqrt{121}$×$\sqrt{9}$=33 | D. | $\sqrt{(-4)^{2}}$=±4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com