
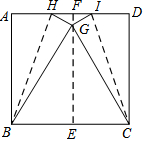
 如圖,將正方形ABCD對折,使點A點與D重合,點B與C重合,折痕EF;展開后再次折疊,使點A與點D重合于正方形內點G處,折痕分別為BH,CI,如果正方形ABCD的邊長是2,則下列結論:①△GBC是等邊三角形;②△IGH的面積是7$\sqrt{3}$-12;③tan∠BHA=2+$\sqrt{3}$;④GE=2$\sqrt{3}$,其中正確的個數有( )
如圖,將正方形ABCD對折,使點A點與D重合,點B與C重合,折痕EF;展開后再次折疊,使點A與點D重合于正方形內點G處,折痕分別為BH,CI,如果正方形ABCD的邊長是2,則下列結論:①△GBC是等邊三角形;②△IGH的面積是7$\sqrt{3}$-12;③tan∠BHA=2+$\sqrt{3}$;④GE=2$\sqrt{3}$,其中正確的個數有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 由折疊的性質得,AB=BG,CD=CG,根據正方形的性質得到AB=BC=CD,等量代換得到BG=BC=CG,推出△GBC是等邊三角形;故①正確;根據正方形的性質得到AD=AB=BC=DC=2;∠D=∠A=90°,由等邊三角形的性質得到∠BGC=60°,GE=$\frac{\sqrt{3}}{2}$BC=$\sqrt{3}$,故④錯誤;推出∠FIG=30°,得到FI=$\sqrt{3}$FG=$\sqrt{3}$(2-$\sqrt{3}$)=2$\sqrt{3}$-3,根據三角形打麻將公式得到△HIG的面積=7$\sqrt{3}$-12,故②正確;根據勾股定理得到AH=HG=$\sqrt{H{F}^{2}+F{G}^{2}}$=4-2$\sqrt{3}$,由三角函數的定義得到tan∠BHA=$\frac{AB}{AH}$=$\frac{2}{4-2\sqrt{3}}$=2+$\sqrt{3}$;故③正確.
解答 解:由折疊的性質得,AB=BG,CD=CG,
∵四邊形ABCD是正方形,
∴AB=BC=CD,
∴BG=BC=CG,
∴△GBC是等邊三角形;故①正確;
∵FE⊥BC,EF⊥AD,
∵四邊形ABCD為正方形,
∴AD=AB=BC=DC=2;∠D=∠A=90°,
又∵將正方形ABCD折疊,使點A與點D重合于正方形內點G處,
∵△GBC為等邊三角形,
∴∠BGC=60°,GE=$\frac{\sqrt{3}}{2}$BC=$\sqrt{3}$,故④錯誤;
∴∠HGI=120°,FG=EF-GE=2-$\sqrt{3}$,
∴∠FIG=30°,
∴FI=$\sqrt{3}$FG=$\sqrt{3}$(2-$\sqrt{3}$)=2$\sqrt{3}$-3,
∴HI=2FI=4$\sqrt{3}$-6,
∴△HIG的面積=$\frac{1}{2}$HI•FG=$\frac{1}{2}$(2-$\sqrt{3}$)(4$\sqrt{3}$-6)
=7$\sqrt{3}$-12,故②正確;
∵AH=HG=$\sqrt{H{F}^{2}+F{G}^{2}}$=4-2$\sqrt{3}$,
∴tan∠BHA=$\frac{AB}{AH}$=$\frac{2}{4-2\sqrt{3}}$=2+$\sqrt{3}$;故③正確;
故選C.
點評 本題考查了折疊的性質:折疊前后的兩圖形全等,即對應角相等,對應線段相等.也考查了正方形和等邊三角形的性質以及含30°的直角三角形三邊的關系.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x≤3 | B. | x≠4 | C. | x≥3或x≠4 | D. | x≤3或x≠4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知OM平分∠AOB,ON平分∠BOC.
如圖,已知OM平分∠AOB,ON平分∠BOC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 方式一 | 方式二 | |
| 月租費 | 30元/月 | 0 |
| 本地通話費 | 0.20元/分鐘 | 0.40元/分鐘 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,己知AB是半徑為2的圓O直徑,C是圓上一點,D是BC延長線上一點,過點D的直線交AC于E點,且△AEF為等邊三角形.
如圖,己知AB是半徑為2的圓O直徑,C是圓上一點,D是BC延長線上一點,過點D的直線交AC于E點,且△AEF為等邊三角形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com