
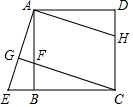
 已知:如圖,在正方形ABCD中,F是AB上一點,延長CB到E,使BE=BF,連接CF并延長交AE于G.
已知:如圖,在正方形ABCD中,F是AB上一點,延長CB到E,使BE=BF,連接CF并延長交AE于G.分析 (1)由于四邊形ABCD是正方形,所以AB=CB=DC,因為AB∥CD,∠CBA=∠ABE,從而得證.
(2)根據旋轉的性質可知△ABE≌△ADH,從而可證AF=CH,然后利用AB∥CD 即可知四邊形AFCH是平行四邊形
解答 (1)證明:∵四邊形ABCD是正方形
∴AB=CB=DC,AB∥CD 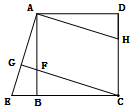 ∠CBA=90°
∠CBA=90°
∴∠ABE=180°-∠ABC=180°-90°=90°
∴∠CBA=∠ABE(等量代換)
在△ABE和△CBF中$\left\{\begin{array}{l}BE=BF\\∠ABE=∠CBF\\ AB=CB\end{array}\right.$
∴△ABE≌△CBF(SAS)
(2)答:四邊形AFCH是平行四邊形
理由:∵△ABE繞點A逆時針旋轉90°得到△ADH
∴△ABE≌△ADH
∴BE=DH
又∵BE=BF(已知)
∴BF=DH(等量代換)
又∵AB=CD(由(1)已證)
∴AB-BF=CD-DH
即AF=CH
又∵AB∥CD 即AF∥CH
∴四邊形AFCH是平行四邊形
點評 本題考查正方形的性質,本題涉及全等三角形的性質與判定,旋轉的性質,平行四邊形的判定,解題的關鍵是證明△ABE≌△CBF與△ABE≌△ADH,本題屬于中等題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
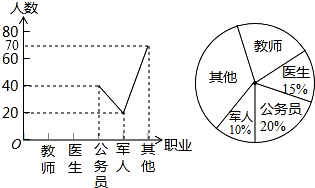 某中學開展以“我最喜歡的職業”為主題的調查活動,通過對學生的隨機抽樣調查得到一組數據,并根據這組數據繪制下面兩幅不完整的統計圖:
某中學開展以“我最喜歡的職業”為主題的調查活動,通過對學生的隨機抽樣調查得到一組數據,并根據這組數據繪制下面兩幅不完整的統計圖:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 兩個大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖形,B,C,E在同一條直線上,連結DC.
兩個大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖形,B,C,E在同一條直線上,連結DC.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
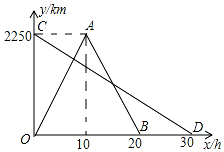 一輛快車和一輛慢車分別從甲、乙兩地同時出發勻速相向而行,快車到達乙地后,原路原速返回甲地.圖1表示兩車行駛過程中離甲地的路程y(km)與行駛時間x(h)的函數圖象.
一輛快車和一輛慢車分別從甲、乙兩地同時出發勻速相向而行,快車到達乙地后,原路原速返回甲地.圖1表示兩車行駛過程中離甲地的路程y(km)與行駛時間x(h)的函數圖象.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,邊長為a,面積為2的正方形放置在數軸上,以原點為圓心,a為半徑,在原點右側用圓規畫出數軸上的一個點A,則點A所表示的實數是$\sqrt{2}$.
如圖,邊長為a,面積為2的正方形放置在數軸上,以原點為圓心,a為半徑,在原點右側用圓規畫出數軸上的一個點A,則點A所表示的實數是$\sqrt{2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com