
 如圖,連結(jié)正五邊形的各條對(duì)角線AD,AC,BE,BD,CE,給出下列結(jié)論:①∠AME=108°;②五邊形PFQNM∽五邊形ABCDE;③AN2=AM•AD,其中正確的是( )
如圖,連結(jié)正五邊形的各條對(duì)角線AD,AC,BE,BD,CE,給出下列結(jié)論:①∠AME=108°;②五邊形PFQNM∽五邊形ABCDE;③AN2=AM•AD,其中正確的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 根據(jù)正五邊形的性質(zhì)得到∠ABE=∠AEB=∠EAD=36°,根據(jù)三角形的內(nèi)角和即可得到結(jié)論;
求證各個(gè)角的度數(shù),再求得各邊的長度,即可得出結(jié)論.
由于∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,得到∠AEN=∠ANE,根據(jù)等腰三角形的判定定理得到AE=AN,同理DE=DM,根據(jù)相似三角形的性質(zhì)得到$\frac{AE}{AD}=\frac{AM}{AE}$,等量代換得到AN2=AM•AD;
解答 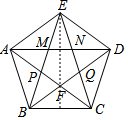 解:∵∠BAE=∠AED=108°,
解:∵∠BAE=∠AED=108°,
∵AB=AE=DE,
∴∠ABE=∠AEB=∠EAD=36°,
∴∠AME=180°-∠EAM-∠AEM=108°,故①正確;
∵∠ABE=∠CBD=36°,
∴∠DBE=36°,
同理∠KMN=∠MNL=∠NLH=∠LHK=∠HKM,
△AMK≌△BMN≌△CNL≌△DHL≌△EHK,
∴MN=NL=LH=HK=MK,
∴五邊形MNLHK是正五邊形,
∴五邊形PFQNM∽五邊形ABCDE,②正確.
∵∠AEN=108°-36°=72°,∠ANE=36°+36°=72°,
∴∠AEN=∠ANE,
∴AE=AN,
同理DE=DM,
∴AE=DM,
∵∠EAD=∠AEM=∠ADE=36°,
∴△AEM∽△ADE,
∴$\frac{AE}{AD}=\frac{AM}{AE}$,
∴AE2=AM•AD;
∴AN2=AM•AD;故③正確;
故選D.
點(diǎn)評(píng) 本題考查了相似三角形的判定和性質(zhì),勾股定理,正五邊形的性質(zhì),熟練掌握正五邊形的性質(zhì)是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
 矩形OABC在平面直角坐標(biāo)系中的位置如圖所示,點(diǎn)B的坐標(biāo)為(3,4),點(diǎn)D是OA的中點(diǎn),點(diǎn)E在線段AB上,當(dāng)△CDE的周長最小時(shí),求點(diǎn)E的坐標(biāo).
矩形OABC在平面直角坐標(biāo)系中的位置如圖所示,點(diǎn)B的坐標(biāo)為(3,4),點(diǎn)D是OA的中點(diǎn),點(diǎn)E在線段AB上,當(dāng)△CDE的周長最小時(shí),求點(diǎn)E的坐標(biāo).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
| A | B | |
| 進(jìn)價(jià)(萬元/.套) | 1.5 | 1.2 |
| 售價(jià)(萬元/套) | 1.65 | 1.4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
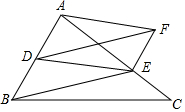 如圖,在△ABC中,D是AB邊上的中點(diǎn),E是AC上一點(diǎn),DF∥BE,EF∥AB,且DF、EF相交于F.
如圖,在△ABC中,D是AB邊上的中點(diǎn),E是AC上一點(diǎn),DF∥BE,EF∥AB,且DF、EF相交于F.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,沿△ABC的各邊想同側(cè)作正三角形ABD、BCF、ACE.
如圖,沿△ABC的各邊想同側(cè)作正三角形ABD、BCF、ACE.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com